Approach your problems from the right end and begin with the answers.
Then one day, perhaps, you will find the final question.
"The Chinese Maze Murders"
by
Robert Hans van Gulik
(1910-1967) It's
better to know some of the questions than all of the answers.
James Grover Thurber
(1894-1961) Whoever answers before pondering the question
is foolish and confused.
Proverbs 18:13
 |
|
- Proof by inspection for finitely applicable statements.
- Only a negative deserves a proof.
- Proving by induction the truth of infinitely many things.
- Stochastic proofs leave only a vanishing uncertainty.
- Heuristic arguments state the likelihood of a conjecture.
- Computer-aided proofs: 4-color theorem (1976).
- Lack of a good approach doesn't invalidate a statement.
- The most interesting theorems are general tools for proving other theorems.
- Treacherous patterns. What holds for a long time may not hold forever.
- Fermat's last theorem: One example of a botched proof.
- All metric prefixes: Current SI prefixes, obsolete prefixes, bogus prefixes...
- Prefixes for units of information (multiples of the bit). Brontobyte hoax.
- Density one. Relative and absolute density precisely defined.
- Acids yielding a mole of H+ per liter are normal (1N) solutions.
- Calories: Thermochemical calorie, gram-calorie, IST calorie (and Btu).
- Horsepowers: hp, metric horsepower and boiler horsepower.
- The standard acceleration of gravity has been 9.80665 m/s2 since 1901.
- Reciprocal time. Frequency (beat) and rate of phase change vs. activity.
Time:
- Tiny durations;
zeptosecond (zs, 10-21s) & yoctosecond (ys, 10-24s).
- A jiffy is either a light-cm or 10 ms (tempons and chronons are shorter).
- A shake (10 ns) is much shorter than two shakes of a lamb's tail.
- The length of a second. Solar time, ephemeris time, atomic time.
- The length of a day. Solar day, atomic day, sidereal or Galilean day.
- Scientific year = 31557600
SI seconds (» Julian year of 365.25 solar days).
Length:
- The International inch (1959) is 999998/1000000 of a US Survey inch.
- The typographer's point is exactly 0.013837" = 0.3514598 mm.
- How far is a league? Land league, nautical league.
- Radius of the Earth and circumference at the Equator.
- Extreme units of length. The very large and the very small.
Surface Area:
- Acres, furlongs, chains and square inches...
Volume, Capacity:
- Capitalization of units. You only have a choice for the liter (or litre ).
- Drops or minims: Winchester, Imperial or metric. Teaspoons and ounces.
- Fluid ounces: US ounces (fl oz) are about 4% larger than British ounces.
- Gallons galore: Winchester (US) vs. Imperial gallon (UK), dry gallon, etc.
- US bushel and Winchester units of capacity (dry = bushel, fluid = gallon).
- Kegs and barrels: A keg of beer is half a barrel, but not just any "barrel".
Mass, "Weight":
- Tiny units of mass. A hydrogen atom is about 1.66 yg.
- Solar mass: The unit of mass in the astronomical system of units.
- Technical units of mass. The slug and the hyl.
- Customary units of mass which survive in the electronic age.
- British weights: Avoirdupois pound & ounce (lb & oz). Troy ounce (ozt).
- The poids de marc system: 18827.15 French grains to the kilogram.
- A talent was the mass of a cubic foot of water.
- Tons: Short ton, long ton (displacement ton), metric ton (tonne), assay ton...
- Other tons: Energy (kiloton, toe, tce), cooling power, thrust, speed.
- Scientific notation: Nonzero numbers given as multiples of powers of ten.
- So many "significant" digits imply a result of limited precision.
- Meaning of inequalities when rounded bounds are involved.
- Standard deviation specifies the uncertainty in the precision of a result.
- Engineering notation reduces a number to a multiple of a power of 1000.
- The quadratic formula is numerically inadequate in common cases.
- Devising robust formulas which feature a stable floating-point precision.
- Underflow: 0.0 stands for a small number not known to be exactly zero.
- The Beaufort scale is now defined strictly in terms of wind speed.
- The Saffir-Simpson Hurricane Scale (SSHS) became a wind scale in 2010.
- The Fujita scale for tornadoes.
- Decibels: A general-purpose logarithmic scale for relative power ratios.
- Sound intensity level (SIL) is well-defined; SPL is an approximation.
- Pitch. An octave is 1200 cents.
- Apparent and absolute magnitudes of stars.
- Acidity. The pH scale was invented by Søren Sørensen in 1909.
- The organoleptic Scoville scale is used to rate the pungency of hot spices.
- Oven temperatures. Cooks may use gas marks or traditional descriptions.
- The Richter scale for earthquakes and other sudden energy releases.
- Volcanic Explosivity Index (VEI) Chris Newhall and Stephen Self (1982).
- Pencil hardness. Clay makes harder graphite leads (lighter swatching).
- The scale of animals according to Galileo Galilei.
- Jumping fleas... compared to jumping athletes...
- Kleiber's law: Metabolic rates of animals as a function of their sizes.
- Drag coefficient of a sphere as a function of the Reynolds number R.
- Benford's Law. Leading digits of quantities expressed in random units.
Model Trains: Scales, gauges & other mathematical aspects.
- Lexicon of railroad jargon: North-American, British and French usage.
- A short history of the scales of model trains...
- Gauges of worldwide lines. 60% are standard gauge (56.5'' = 1.4351 m).
- Gauges of model tracks. HO and OO models can share the same tracks.
- Types of model trains. Naming usual combinations of a scale and a gauge.
- Large model trains are often used outdoors. Some are ridable.
- Gauges are almost in geometric progression: Z,N,TT, HO, S,O,1,3...
- The height of a miniature rail, in thousands of an inch, is called its code.
- Composition of modern miniature rails: Nickel-silver contains no silver.
- Travelage is the number of crossties per unit of distance.
- Luminous power of sources at scale 1/s should be 1/s2 that of prototypes.
- Scenery scale. 81 is the geometric mean between 87 (HO) and 76 (OO).
- Mirrors and shadows. Overlooked aspects of scenery in confined spaces.
- Couplers.
- Loading gauge.
- Radius of curved track available from different manufacturers.
- Least separation between curved parallel tracks, for specific rolling stock.
- Turnouts. The frog number is the cotangent of the frog angle.
- Sectional tracks. The need for compensator and/or correctors.
- DC control. Traditional control of model trains, by Direct current.
- DCC. Digital command control of several locomotives on the same track.
- Sound. Some DCC locomotives feature on-board sound effects.
- Blocks. A layout can be divided into blocks powered separately.
- Detection & transponding. Locomotives located by the power they use.
- OpenLCB (NMRAnet). Local control bus = Control area network (CAN).
- Famous trains and locomotives and their miniature counterparts.
- Dream lines. Legendary railroad services, past and present.
- A quick survey of a few grand layouts. Great modeling achievements.
Physical Constants:
- For the utmost in precision, physical constants are derived in a certain order.
- Primary conversion factors between customary systems of units.
6+1 Basic Dimensionful Physical Constants (Proleptic SI)
- Speed of Light in a Vacuum (Einstein's Constant): c = 299792458 m/s.
- Magnetic Permeability of the Vacuum: An exact value defining the ampere.
- Planck's constant: The ratio of a photon's energy to its frequency.
- Boltzmann's constant: Relating temperature to energy.
- Avogadro's number: The number of things per mole of stuff.
- Mechanical equivalent of light (683 lm/W @ 540 THz) defines the lumen.
- Newton's constant of gravitation and a futuristic definition of the second.
Dimensionless Physical Constants:
- Galileo's constant. What Galileo measured
is now known to be 8 / p2
- Sommerfeld's fine-structure constant
a = 1 / 137.036 (or so).
- The large number W. A dimensionless number pondered by Dirac.
Fundamental Mathematical Constants:
- 0: Zero is the most fundamental and most misunderstood of all numbers.
- 1 and -1: The unit numbers.
- p ("Pi"): The ratio of the circumference of a circle to its diameter.
- Ö2: The diagonal of a square of unit side. Pythagoras' Constant.
- Ö3: Diameter of a cube of unit side. Constant of Theodorus.
- f: The diagonal of a regular pentagon of unit side. The Golden Number.
- Euler's e: Base of the exponential function which equals its own derivative.
- 63.2% (1-1/e) of a sudden level shift is achieved after one time constant.
- ln(2): The alternating sum of the reciprocals of the integers.
- An engineering favorite: The decimal logarithm of 2.
- Euler-Mascheroni Constant g :
Limit of [1 + 1/2 + 1/3 +...+ 1/n] - ln(n).
- Catalan's Constant G : The alternating sum of the reciprocal odd squares.
- Apéry's Constant z(3) : The sum of the reciprocals of the perfect cubes.
- Imaginary i: If "+1" is a step forward, "+ i" is a step sideways to the left.
Exotic Mathematical Constants:
- Delian constant: 21/3 is the solution to the duplication of the cube.
- Gauss's constant: Reciprocal of the arithmetic-geometric mean of 1 and Ö2.
- Rayleigh factor for the diffraction limit of angular resolution.
- Mertens constant: The limit of [1/2 + 1/3 + 1/5 +...+ 1/p] - ln(ln p)
- Artins's constant is the proportion of long primes in decimal or binary.
- Ramanujan-Soldner constant (m): Positive root of the logarithmic integral.
- Landau-Ramanujan constant. Asymptotic density of sums of two squares.
- The Omega constant: W(1) is the solution of the equation x exp(x) = 1.
- Feigenbaum constant (d) and the related reduction parameter (a).
- Fransén-Robinson constant: Inverse-Gamma integral.
- Landau's constant.
- Bloch's constant.
Some Third-Tier Mathematical Constants:
- Gelfond's Constant raised to the power of i is -1.
- Brun's Constant: A standard uncertainty (s)
means a 99% level of ±3s
- Prévost's Constant: The sum of the reciprocals of the Fibonacci numbers.
- Grossman's Constant: One recurrence converges for only one initial point.
- Ramanujan's Number: exp(p Ö163) is almost an integer.
- Viswanath's Constant: Mean growth in random additions and subtractions.
- Copeland-Erdös Number: Almost all numbers are normal, like this one.
- Always change your first guess if you're always told another choice is bad.
- The Three Prisoner Problem predated Monty Hall and Marilyn by decades.
- Seating N children at a round table in (N-1)! different ways.
- How many Bachet squares? A 1624 puzzle using the 16 court cards.
- Choice Numbers: C(n,p) is the number of ways to choose p items among n.
- Multichoice Numbers: Putting n objects into distinct boxes of fixed sizes.
- C(n+p-1,p) distinct ways to put p identical balls into n numbered bins.
- C(n+2,3) three-scoop sundaes. Several ways to count them (n flavors).
- C(n+p-1,p) choices of p items among n different types, allowing duplicates.
- How many new intersections of straight lines defined by n random points.
- Catalan numbers are the results of many different enumerations.
- Face cards. The probability of getting a pair of face cards is less than 5%.
- Homework Central: Aces in 4 piles, bad ICs, airline overbooking.
- Binomial distribution. Defective units in a sample of 200.
- Siblings with the same birthday. What are the odds in a family of 5?
- Covariance: A generic example helps illustrate the concept.
- Variance of a binomial distribution, derived from general principles.
- Standard deviation. Two standard formulas to estimate it.
- Markov's inequality is used to prove the Bienaymé-Chebyshev inequality.
- Bienaymé-Chebyshev inequality: Valid for any probability distribution.
- Inclusion-Exclusion: One way to find the probability of a union of 3 events.
- The "odds in favor" of poker hands: A popular way to express probabilities.
- Probabilities of a straight flush in 7-card stud (generalized to "q-card stud").
- Probabilities of a straight flush among 26 cards (or any other number).
- The exact probabilities in 5-card, 6-card, 7-card, 8-card and 9-card stud.
- Rearrangements of CONSTANTINOPLE so no two vowels are adjacent...
- Four-letter words from POSSESSES: Counting with generating functions.
- How many positive integers below 1000000 have their digits add up to 19?
- Polynacci Numbers: Flipping a coin n times without p tails in a row.
- Winning in finitely many flips or losing endlessly...
- 252 decreasing sequences of 5 digits (2002 nonincreasing ones).
- How many ways are there to make change for a dollar? Closed formulas.
- Partitioniong an amount into the parts minted in a certain currency.
- The number of rectangles in an N by N chessboard-type grid.
- The number of squares in an N by N grid: 0, 1, 5, 14, 30, 55, 91, 140...
- Screaming Circles: How many tries until there's no eye contact?
- Average distance between two random points on a segment, a disk, a cube...
- Average distance between two points on the surface of a sphere.
- Normal sequences feature any string with equal probability.
- Fair coin generated from the output of a Geiger counter.
- Random integer below n generated from a fair coin.
- Burning cards may defeat cheating but doesn't affect random outcomes.
- Shuffling cards to give every permutation the same probability.
- Legally cheating at online poker by taking advantage of poor programming.
- Probability distributions: Measurability.
- Bayes' Theorem. A formula which applies to classical probabilities.
- The Bayesian universe: Probabilities quantify beliefs.
- Aggregation paradox: Confusion factors and meaningless correlations.
- Raw product ratings. How do they compare to each other?
- Quantum theory is not Bayesian.
- The human brain is not a Bayesian engine but there's still hope...
- Short history of playing cards: From China to Europe, to the New World.
- Sizes of playing cards: French, Bridge, Poker, French tarot, Patience, etc.
- How playing cards are made: Either 2 layers of paper or 100% plastic.
- Suits: Spades, hearts, diamonds & clubs (swords, cups, coins & wands).
- The four court cards: Ace, king, queen, jack (king, queen, cavalier, page).
- The Mameluke 52-card standard deck with 3 figure cards per suit.
- 78-card tarot deck: 21 trumps, 1 fool, 4 suits of 14 (incl. 4 court cards).
- The Major Arcana: Trumps and fool of the tarot deck, in occult parlance.
- Names of the court cards in the French tradition. Hundred Years' War.
- 48-card Aluette deck: Latin suits, mimicks and names of special cards.
- Jokers from Euchre (1857) found their way into Poker in the 1870's.
- The 40-card Spanish baraja deck lacks 8, 9 & 10.
- The 32-card piquet deck lacks 2-6.
French Belote and German Skat.
- Skat: The most popular German card game (32-card deck).
- 24-card deck for Euchre (single deck) and Pinochle (double deck).
- Happy Families: 44-card British deck of 11 families of 4 (1851).
- Jeu des 7 familles: 42-card French deck of 7 families of 6 (1876).
- 1000 Bornes: 106 cards for a boardless car-racing game (1954).
- Set® cards: Combinatorics of a modern 81-card ternary deck (1974).
- New-deck order for the whole 81-card SET deck (or the 27 solids only).
- Zener cards were invented in the early 1930s for (deprecated) ESP tests.
- Gaming chips: Color coding, shapes & sizes, designs. Jetons & plaques.
- Casino edge: Gambling beyond the cost of entertainement is foolish.
- Faro was the most popular banking game from 1825 to 1915.
- Baccarat (Punto-Banco).
- EZ Baccarat(™). The original Dragon-7 and newer Panda-8 side bets.
- Carribean Stud.
- Three-Card Poker.
- Glossary: A few specialized term used in blackjack.
- Casino rules for Blackjack.
- Basic strategy against an infinite shoe.
- Pair of aces (soft 12). What to do if you're not allowed to split it?
- Blackjack enumerations using polynomials.
- History of Blackjack counting.
Poker 101 : Rules, Odds & Glossary
- 5-card draw: The simplest form of poker is the basis for video poker.
- The 2598960 poker hands come in 9 or 10 types, rarest ones first.
- Kickers may help break ties between hands bearing the same name.
- Perfect Poker: "Deuces or better" have 1 to 1 odds with the full-wheel rule.
- Poker chips: Color, size and weight.
- Poker chip sets: Practical repartitions into various denominations.
- Structure sheet of the most exclusive invitation-only tournament.
- Handling chips: Counting them, stacking them, betting with them.
- Poker chip tricks.
- 7-card stud was the most popular variant of poker before NLHE and PLO.
- 7-card combos: Odds of best 5-card hands extracted from 7 random cards.
- Betting rules: Antes & blinds, checking, opening, calling and raising.
- Glossary: The jargon of poker.
Poker 102 : No-Limit Hold 'em & Pot-Limit Omaha
- Texas hold 'em: Two hole cards (hand) and five community cards (board).
- Preflop probabilities (win or tie a showdown) for all 169 starting hands.
- If you have kings in an m-handed game, how often do you run into aces?
- Trips or quads from a lone board pair.
- With 3 clubs on the board: If a player has a flush, does someone else?
- Nontransitivity of matches: Pairwise showdowns can be inconsistent.
- How much to bet depends on the goal (make money or avoid elimination).
- Omaha Hold 'em: Use 2 hole cards (out of 4) and 3 board cards (out of 5).
- Poisson Processes: Random arrivals happening at a constant rate (in Bq).
- Simulating a poisson process with a uniform random number generator.
- Markov Processes: When only the present influences the future...
- The Erlang B Formula assumes callers don't try again after a busy signal.
- Markov-Modulated Poisson Processes may look like Poisson processes.
- The Utility Function: A dollar earned is usually worth less than a dollar lost.
- St. Petersburg's Paradox: What would you pay to play the Petersburg game?
- Two-envelope problem. Don't misuse random variables !
- Sperner's lemma. A discrete version of Brouwer's fixed-point theorem.
- Sharing a necklace with N types of beads, in just N cuts.
- One man, one vote! That's conclusive only when there are just two options.
- The case for a rigorous approach, when the majority rule doesn't suffice.
- Condorcet's Paradox: A group of rational voters need not behave rationally.
- Tallying systems based on additive preference points are misguided at best.
- Plurality voting is just another point-system, possibly the worst of them.
- Runoff systems: Ad hoc improvements on plurality voting.
- The Borda method, the foremost point system, is finally being phased out.
- Cardinal voting could usefully supplement ordinary ordinal voting.
- Conform Condorcet methods always produce the right choice, if it's clear.
- Llull's method turns any preliminary order into a conform voting system.
- Tallies: Summaries of voting data that allow the outcome to be computed.
- Manipulations: Taking advantage of the weaknesses of a voting system.
- A composite system aggregating preference lists and discretionary points.
- Stability of a slate and stabilization of slate primaries..
- Incumbents play a key rôle in any political election.
- Aggregating lists of preferences from voters, when that's all we have...
- Voter transition matrix from a primary to a general election.
- Copeland scores provide an appealing conform Condorcet tally.
- The second-order Copeland tallying method has some theoretical virtues.
- The Schulze method uses a transitive relation based on voter wishes.
- Apportioning whole numbers in lieu of fractional values, for a given total.
- The Big Picture: What an elected government should and should not do.
- Center of an arc determined with straightedge and compass.
- Surface areas: Circle, trapezoid, triangle, sphere, frustum, cylinder, cone...
- Simson line of a circumcircle point contains its projections along the sides.
- Isogonal conjugates Concurrent bissector reflections of concurrent lines.
- Euler's line goes through the orthocenter, the centroid and the circumcenter.
- Euler's circle is tangent to the incircle and the excircles (Feuerbach, 1822).
- Power of a point with respect to a circle (Jakob Steiner, 1826).
- Ptolemy's theorem relates the diagonals and the sides of a cyclic tetragon.
- Barycentric coordinates & trilinears exemplify homogeneous coordinates.
- Elliptic arc: Length of the arc of an ellipse between two points.
- Perimeter of an ellipse. Exact formulas and simple ones.
- Surface of an ellipse.
- Volume of an ellipsoid (either a spheroid or a scalene ellipsoid).
- Surface area of a spheroid (oblate or prolate ellipsoid of revolution).
- Quadratic equations in the plane describe ellipses, parabolas, or hyperbolas.
- Centroid of a circular segment. Find it with Guldin's (Pappus) theorem.
- Parabolic arc of given extremities with a prescribed apex between them.
- Focal point of a parabola. y = x 2 / 4f (where f is the focal distance).
- Parabolic telescope: The path from infinity to focus is constant.
- Make a cube go through a hole in a smaller cube. Prince Rupert's paradox.
- Octagon: The relation between side and diameter.
- Constructible regular polygons and constructible angles (Gauss).
- Areas of regular polygons of unit side: General formula & special cases.
- For a regular polygon of given perimeter, the more sides the larger the area.
- Curves of constant width: Reuleaux Triangle and generalizations.
- Irregular curves of constant width. With or without any circular arcs.
- Solids of constant width. The three-dimensional case.
- Constant width in higher dimensions.
- Fourth dimension. Difficult to visualize, but easy to consider.
- Volume of a hypersphere and hyper-surface area, in any dimensionality.
- Hexahedra. The cube is not the only polyhedron with 6 faces.
- Descartes-Euler Formula: F-E+V=2 but restrictions apply.
- Symmetries of the plane. Another approach to Euclidean axioms.
- Napoleon's theorem: Three equilateral triangles around a scalene triangle...
- Morley's theorem: The 3 intersections of adjacent trisectors are equidistant.
- 6-point Conway circle. Every vertex prolongated by the opposite distance.
- Polarity: A geometric duality due to Apollonius of Perga (c. 200 BC).
- The invention of perspective by Renaissance artists.
- Projective spaces: Projective line, projective plane, etc.
- Homogeneous coordinates. Feuerbach, Möbius, Plücker (1827 & 1828).
- Projective duality: Points are incident to lines. Lines are incident to points.
- Pappus' theorem.
- Pascal's theorem was proven by Blaise Pascal when he was 16.
- Brianchon's theorem: The dual of Pascal's theorem.
- Desargues' theorem (c. 1639).
- The two cyclic points (I and J) of Jean-Victor Poncelet (1820).
- Fano plane PG(2,2). Projective geometry in dimension 2 and order 2.
- Metric spaces: The motivation behind more general topological spaces.
- Abstract topological spaces are defined by calling some subsets open.
- Limits in abstract topological spaces.
- Nets (generalized sequences). Moore-Smith sequences (1922).
- Basis of a topology: A set is open iff it's a union of sets from the base.
- Closed sets are sets (of a topological space) whose complements are open.
- Subspace F of E: Its open sets are the intersections with F of open sets of E.
- Separation axioms: Flavors of topological spaces, according to Trennung.
- Compactness of a topological space: Any open cover has a finite subcover.
- Paracompact space: Any open cover has a locally-finite open refinement.
- Locally compact sets contain a compact neighborhood of every point.
- Extreme-value theorem: The continuous image of a compact is compact.
- Borel sets. Tribes form the topological foundation for measure theory.
- General properties of sequences characterize topological properties.
- Continuous functions let the inverse image of any open set be open.
- Homeomorphic spaces. An homeomorphism is a bicontinuous function.
- Hilbert curve. A continuous function from ]0,1[ to the square ]0,1[×]0,1[.
- Restrictions remain continuous. Continuous extensions may be impossible.
- The product topology makes projections continuous on a cartesian product.
- Connected sets can't be split by open sets. The empty set is connected.
- Intermediate-value theorem.
- Path-connected sets are a special case of connected sets.
- Arc-connected spaces are path-connected. The converse need not be true.
- Homotopy: A progressive transformation of a function into another.
- The fundamental group: The homotopy classes of all loops through a point.
- Homology and Cohomology. Poincaré duality.
- Descartes-Euler Formula: F-E+V = 2, but restrictions apply.
- Euler Characteristic: c (chi) extended beyond its traditional definition...
- Winding number of a continuous planar curve about an outside point.
- Fixed-point theorems by Brouwer, Shauder and Tychonoff.
- Turning number of a planar curve with a well-defined oriented tangent.
- Real projective plane and Boy's surface.
- Classification Theorem for connected closed surfaces.
- Hadwiger's additive continuous functions of d-dimensional rigid bodies.
- Eversion of the sphere. An homotopy can turn a sphere inside out.
- Classification of surfaces: "Zero Irrelevancy Proof" (ZIP) by J.H. Conway.
- Braid groups: Strands, braids and pure braids.
- Zariski topology (algebraic geometry). Only algebraic subsets are closed.
- Fiber bundles and fibrations. Locally homeomorphic to a direct product.
- Complete metric space: A space in which all Cauchy sequences converge.
- Continuity and uniform continuity.
- Uniformity is sufficient to define completeness (or lack thereof).
- Flawed alternatives to completeness.
- Banach spaces are complete normed vector spaces.
- Fréchet spaces are generalized Banach spaces.
- Fractional exponents were first conceived by Nicole d'Oresme (c. 1360).
- The von Koch curve (and snowflake): Dimension of self-similar objects.
- The Julia set and the Fatou set of an analytic function are complementary.
- The Mandelbrot set was so named by Adrien Douady & John H. Hubbard.
- Hausdorff dimension is revealed by a covering with balls of radius < e.
- Planar angles (from one direction to another) are signed quantities.
- Bearing: Unless otherwise specified, this is the angle west of north.
- Solid angles are to spherical patches what planar angles are to circular arcs.
- Circular measures: Angles and solid angles aren't quite dimensionless...
- Solid angle formed by a trihedron : Van Oosterom & Strackee (1983).
- Solid angle subtended by a rhombus. Apex of a right rhombic pyramid.
- Formulas for solid angles subtended by patches with simple shapes.
- Right ascension and declination. Precession of celestial coordinates (a,d).
- Curvature of a planar curve: Variation of inclination with distance dj/ds.
- Curvature and torsion of a three-dimensional curve.
- Distinct curvatures and geodesic torsion of a curve drawn on a surface.
- The two fundamental quadratic forms at a point of a parametrized surface.
- Lines of curvature: Their normal curvature is extremal at every point.
- Geodesic lines. Least length is achieved with zero geodesic curvature.
- Meusnier's theorem: Tangent lines have the same normal curvature.
- Mean curvature at a point: Half-sum of the two principal curvatures.
- Gaussian curvature of a surface. The Gauss-Bonnet theorem.
- Parallel-transport of a vector around a loop. Holonomic angle of a loop.
- Total curvature of a curve. The Fary-Milnor theorem for knotted curves.
- Linearly independent components of the Riemann curvature tensor.
- Cartesian equation of a straight line passing through two given points.
- Confocal Conics: Ellipses and hyperbolae sharing the same pair of foci.
- Spiral of Archimedes: Paper on a roll, or groove on a vinyl record.
- Hyperbolic spiral: The inverse of the Archimedean spiral.
- Catenary: The shape of a thin chain under its own weight.
- Tractrix: Meridian of Beltrami's pseudosphere. Involute of the catenary.
- Witch of Agnesi. How the versiera (Agnesi's cubic) got a weird name.
- Folium of Descartes.
- Lemniscate of Bernoulli: A quartic curve shaped like the infinity symbol.
- Cassini oval: The product of the distances to the two foci is constant.
- Limaçons of Pascal: The cardioid (unit epicycloid) is a special case.
- Cartesian oval: The weighted average distance to two poles is constant.
- The envelope of a family of curves is everywhere tangent to one of them.
- The evolute of a curve is the locus of its centers of curvature.
- Involute of a curve: Trajectory of a point of a line rolling on that curve.
- Parallel curves share their normals, along which their distance is constant.
- The nephroid (or two-cusped epicycloid ) is a catacaustic of a circle.
- Freeth's nephroid: A special strophoid of a circle.
- Bézier curves are algebraic splines. The cubic type is the most popular.
- Piecewise circular curves: The traditional way to specify curved forms.
- Intrinsic equation [curvature as a function of arc length] may have spikes.
- The quadratrix (trisectrix) of Hippias squares the circle and trisects angles.
- The parabola is constructible with straightedge and compass.
- Mohr-Mascheroni constructions use the compass alone (no straightedge).
- Osculating curves. Beautiful extensions of the Tait-Kneser theorem.
- Cartesian equation of a plane, knowing its closest point from the origin.
- Helicoid. Surface of minimal area first studied by Meusnier in 1776.
- Ruled surfaces: Cone, conic hyperboloid, helicoid, etc.
- Developable surfaces.
- Surfaces of revolution: Parallel and meridians are lines of curvature.
- Guldin's theorems: Surface area and volume of a solid of revolution.
- Euler's catenoid: Surface of revolution of least surface area.
- Surfaces of constant mean curvature (CMC). The shapes of soap film.
- Beltrami's pseudosphere: Surface of revolution with constant curvature.
- Quadric surfaces = quadratic equations (degree n-1 in n dimensions).
- Perfect monkey saddle: A minimal surface with ternary axial symmetry.
- Convex combinations of two surfaces.
- Dual pair of surfaces.
- Intrinsic equation of a surface.
- Glossary of terms related to gears.
- Gear ratio: Ratio of the input rotation to the output rotation (signed).
- Planar curves rolling without slipping while rotating about two fixed points.
- Congruent ellipses roll against each other while revolving around their foci.
- Elliptic gears: A family of gears which include ellipses and sine curves.
- Watchmaker gears: Ogival surfaces for pinions & radial planes for wheels.
- La Hire's theorem : An hypocycloid of ratio 2 is a straight line.
- Cycloidal gear: Epicycloidal addendum curve & hypocycloidal dedendum.
- The law of conjugate action was formulated by Leonhard Euler (c. 1754).
- Involute tooth profiles provide a uniform rotational speed ratio.
- Harmonic Drive: A flexspline with 2 fewer teeth than the circular spline.
- Circular arc helical gears: E. Wildhaber (1923) & M.L. Novikov (1956).
- Double circular arc helical gears were standardized by the Chinese in 1981.
- Sidereal time: 46879 sidereal days = 46751 mean solar days.
- Daniels coaxial escapement: A major horological innovation.
- Hexahedra. The cube is not the only polyhedron with 6 faces.
- Fat tetragonal antiwedge: Chiral hexahedron of unit volume and least area.
- Duality: To a face of a polyhedron corresponds a vertex of its dual.
- Enumeration of polyhedra: Convex polyhedra with n faces and k edges.
- The 5 Platonic solids: Cartesian coordinates of the vertices.
- Symmetries may equate all commensurate components of a polyhedron.
- Equimetric polyhedra feature constant measures for all elements of a kind.
- There are 75 or 76 nonprismatic uniform polyhedra (18 of them convex).
- The 13 Archimedean solids and their duals (Catalan solids).
- Every isogonal family is typified by a uniform polyhedron.
- Polyhedra in certain families are named after one prominent polygon.
- Some special polyhedra may have a traditional (mnemonic) name.
- Deltahedra have equilateral triangular faces. Only 8 deltahedra are convex.
- Johnson Polyhedra and the associated nomenclature.
- Polytopes are the n-dimensional counterparts of 3-D polyhedra.
- A simplex of touching unit spheres may allow a center sphere to bulge out.
- Regular Antiprism: Height and volume of a regular n-gonal antiprism.
- The Szilassi polyhedron features 7 pairwise adjacent hexagonal faces.
- Wooden buckyball: Cutting 32 blocks to make a truncated icosahedron.
- Zonogons, zonohedra, zonotopes. Zones and zonoids.
- Plesiohedra are space-filling: Cuboctahedron, truncated octahedron, etc.
- Pyritohedron: One dodecahedral pentagonal isohedron is space-filling.
- 16 possible standard dice (opposite faces add up to 7). Two handedness.
- 30 labelings of a die: For 16 of them, opposite faces never add up to 7.
- 3-sided spindle: A 9-hedron with 6 unstable faces.
- Nontransitive dice: Every die is dominated by another die from the set.
- Sicherman dice yield any total with the same probability as a regular pair.
- Percentile dice and other ways several dice can have equiprobable sums.
- Polyhedral dice were popularized by rôle playing games.
- Commonly available dice sizes: Small, medium, large, jumbo and giant.
- Convex isohedra are fair dice, by reason of symmetry between faces.
- Round dice: Outer isohedral marks & steel ball in an isogonal cavity.
- Scalene isogonal polyhedra. Their duals are scalene isohedra.
- Juryeonggu: Korean die with 8 hexagonal faces and 6 square ones.
- Fairness of a non-isohedral die may depend on the way it's tossed.
- Are there any intrinsically fair dice which aren't isohedral?
- Necessary conditions an absolutely fair die must satisfy.
- Quasistatic probability is proportional to the solid angle a face subtends.
- Thermal tossing puts a face of minimal height at the bottom.
- Balanced mesohedral dice are fair for both quasistatic and thermal tossing.
- Mesodecahedron: Mesohedron with 10 faces.
- Mesopentahedron: The mesohedral proportions of a rhombic pyramid.
- Mesoheptahedron: Mesohedron with 7 faces.
- Statistical bias of unfair dice.
Isohedra. The symmetry of fair dice.
- Classification of all convex isohedra. Intrinsic fair dice.
- Disphenoids are tetrahedra where opposing edges have equal length.
- The hexakis icosahedra (120 faces) include the disdyakis triacontahedra.
- Two chiral fair dice: No mirror symmetry, 24 or 60 pentagonal faces.
- A pseudo-isohedral die. Its faces are congruent, but is it fair?
- The bridges of Königsberg: Eulerian graphs and the birth of graph theory.
- Undirected graphs are digraphs with symmetrical adjacency matrix.
- Adjacency matrix of a directed graph (digraph) or of a bipartite graph.
- The 3-utilities problem: Providing 3 cottages with water, gas & electricity.
- Silent Circles: An enumeration based on adjacency matrices (Alekseyev).
- Silent Prisms: Modifying the screaming game for short-sighted people.
- Tallying markings of one edge per node where no edge is marked twice.
- Line graph: Nodes of L(G) are edges of G (connected iff adjacent in G).
- Transitivity: Vertex-transitive and/or edge-transitive graphs.
- Desargues graph and distance transitivity.
- Tensor product of two graphs (directed or not).
- Hedetniemi's conjecture (1966). Disproved by Yaroslav Shitov, in 2019.
- The brain as a graph. Blue-Brain project (2005-) of Henry Markam.
- Heterosexuality: Male promiscuity is the same as female promiscuity!
- Factorial zero is 1, so is an empty product. An empty sum is 0.
- Anything to the power of 0 is equal to 1, including 0 to the power of 0.
- Zero is divisible by anything but it divides only itself!
- Idiot's Guide to Complex Numbers.
- Using the Golden Ratio (f) to express the 5 [complex] fifth roots of unity.
- "Multivalued" functions are functions defined over a Riemann surface.
- Square roots are inherently ambiguous for negative or complex numbers.
- The difference of two numbers, given their sum and their product.
- All symmetric polynomials of 3 variables are determined by the first three.
- Geometric progression of 6 terms. Sum is 14, sum of squares is 133.
- Quartic equation involved in the classic "Ladders in an Alley" problem.
- Chebyshev polynomials express
cos nq as a function of cos q
- Chebyshev polynomials of the second kind obey the same recurrence...
- Legendre polynomials and zonal harmonics.
- Laguerre polynomials. Hypergeometric confluent function.
- Hermite polynomials. Eigenstates of the quantum harmonic oscillator.
- Bessel polynomials.
- Bernoulli polynomials.
- Faulhaber polynomials.
- Euler polynomials.
- Mittag-Leffler polynomials.
- Cyclotomic polynomials are irreducible over the rationals.
- Lucas coefficients form polynomials dividing cyclotomic polynomials.
- The Art of Polynomial Factorizations. Manufacturing remarkable identities.
- Permutation matrices include the identity matrix and the exchange matrix.
- Gil's matrix. The favorite square matrix of professor W. Gilbert Strang.
- Operations on matrices are conveniently defined using Dirac's notation.
- Triangular matrices. Proper isomorphism between upper and lower ones.
- The determinant is proportional to any completely antisymmetrical form.
- Minors. First minors are obtained by deleting one row and one column.
- Adjugate of a matrix: Transpose of its cofactor matrix A adj(A) = det(A) I
- Eigenvectors and eigenvalues of an operator or a matrix.
- The numerical range of a complex matrix. Locus of its Rayleigh ratios.
- The characteristic polynomial of an operator doesn't depend on the basis.
- The minimal polynomial has the same zeroes but no multiple roots.
- Cayley-Hamilton theorem: A matrix vanishes its characteristic polynomial.
- Normal matrices and diagonalizable matrices.
- Totally positive generalized Vandermonde matrices (fractional powers).
- Cholesky decomposition L L* of an Hermitian matrix.
- Toeplitz matrix: Constant diagonals.
- Circulant matrix: Cyclic permutations of the first row.
- Linear recurrences of order k-1 which define sequences of period k.
- Wendt's Determinant: The circulant of the binomial coefficients.
- Hankel matrix: Constant skew-diagonals.
- Catberg matrix: Hankel matrix of the reciprocal of Catalan numbers.
- Hadamard matrix: Unit elements and orthogonal columns.
- Sylvester matrix of two polynomials has their resultant for determinant.
- The discriminant of a polynomial is the resultant of itself and its derivative.
- Pfaffian: Polynomial whose square equals an antisymmetric determinant.
- The numerical range of a complex matrix. Locus of its Rayleigh ratios.
- Matrices with coefficients in a noncommutative ring.
- Matrix exponential. The exponential of a matrix is an invertible matrix.
- Matrix gamma function. The reciprocal gamma is an entire function.
- Matrix Mittag-Leffler functions. Applications to fractional calculus.
- Values of analytic functions for nilpotent matrices reduce to finite sums.
- Trigonometric functions: Memorize a simple picture for 3 basic definitions.
- Solving triangles with the law of sines, law of cosines & law of tangents.
- Spherical trigonometry: Triangles drawn on the surface of a sphere.
- Sum of tangents of two half angles, in terms of sums of sines and cosines.
- The absolute value of the sine of a complex number.
- All positive rationals (& square roots) as trigonometric functions of zero!
- Function types: Polynomial, rational, algebraic, transcendental, special.
- Exact solutions to transcendental equations.
- The sine function: How to compute it numerically.
- Chebyshev economization saves billions of steps in common computations.
- The Gamma function: Its definitions, properties and special values.
- Lambert's W function is used to solve practical transcendental equations.
- Dilogarithm, trilogarithm and polylogarithms. Jonquière's function.
- Deformed exponential function. Entire function with a complex parameter.
- The Gamma function: Its definitions, properties and special values.
- Euler's integral of the second kind can define G(z) when Re(z) > 0.
- Euler's reflection formula.
G(z) G(1-z) = p / sin pz .
- Stirling's approximation: An asymptotic expansion for factorials.
- Stirling's expansion is a divergent asymptotic series.
- Hölder's theorem: G doesn't satisfy any algebraic differential equation.
- Kümmer's series and the integral representation of Log G (x).
- Knar's formula.
- Euler's beta function (Euler, 1730). Euler integral of the first kind. B(x,y).
- Digamma (Gauss' psi-function): Logarithmic derivative of G.
- Pochhammer's symbol: Upper factorial of k increasing factors: x(x+1)...
- Gauss's hypergeometric function: 2+1 parameters (and one variable).
- Kummer's transformations relate different hypergeometric expressions.
- Sum of the reciprocal of Catalan numbers, in closed hypergeometric form.
- Appell series. Two-variable generalizations.
- WZ pairs. Zeilberger's algorithm. Gosper's algorithm.
 Prototypical theta function.
Prototypical theta function.
- Legendre's elliptic integrals.
- Carlsons's canonical symmetric elliptic integrals.
- Jacobi theta functions:
- q-analogs.
- Ramanujan theta function.
- False theta functions, (L.J. Rogers, 1894, 1917).
- Mock theta functions were introduced by S. Ramanujan, in 1920.
- Partial theta functions.
- Circumference of an ellipse: Exact series and approximate formulas.
- Ramanujan I and Lindner formulas: The journey begins...
- Ramanujan II: An awesome approximation from a mathematical genius.
- Hudson's Formula and other Padé approximations.
- Peano's Formula: The sum of two approximations with cancelling errors.
- The YNOT formula (Maertens, 2000. Tasdelen, 1959).
- Euler's formula is the first step in an exact expansion.
- Naive formula: p
( a + b ) features a -21.5% error for elongated ellipses.
- Cantrell's Formula: A modern attempt with an overall accuracy of 83 ppm.
- From Kepler to Muir. Lower bounds and other approximations.
- Relative error cancellations in symmetrical approximative formulas.
- Complementary convergences of two series. A nice foolproof algorithm.
- Elliptic integrals & elliptic functions. Traditional symbols vs. computerese.
- Padé approximants are used in a whole family of approximations...
- Improving Ramanujan II over the whole range of eccentricities.
- The Arctangent Function as a component of several approximate formulas.
- Abed's formula uses a parametric exponent to fine-tune the approximation.
- Zafary's formula. Improved looks for a brainchild of Shahram Zafary.
- Rivera's formula gives the perimeter of an ellipse with 104 ppm accuracy.
- Better accuracy from Cantrell, building on his own previous formula
- Rediscovering a well-known exact expansion due to Euler (1773).
- Exact expressions for the circumference of an ellipse: A summary.
- Surface Area of a Scalene Ellipsoid: The general formula isn't elementary.
- Thomsen's Formula: A simple symmetrical approximation.
- Approximate formulas for the surface area of a scalene ellipsoid.
- Nautical mile: "Average" minute of latitude on an oblate spheroid.
- Great ellipses have the same center as the ellipsoid they are drawn on.
- Area enclosed by a curve drawn on the surface of an oblate spheroid.
- Pseudo-straight boundaries of areas varying quadratically with longitude.
- Derivative: The slope of a function and/or something more abstract.
- The logarithmic derivative of a product is the sum of those of its factors.
- Integration: The Fundamental Theorem of Calculus.
- Integration by parts: Reducing an integral to another one.
- Wallis' integrals. Integration by parts yields a recurrence relation.
- Length of a parabolic arc.
- Top height of a curved bridge with a 5280 ft span and a 5281 ft length.
- Sagging: A cable which spans 28 m and sags 30 cm is 28.00857 m long.
- The length of the arch of a cycloid is 4 times the diameter of the wheel.
- Integrating the cube root of the tangent function.
- Changing inclination for a particle moving along a parabola.
- Algebraic area of a figure 8 may be the sum or the difference of its lobes.
- Area surrounded by an oriented planar loop which may intersect itself.
- Linear differential equations of higher order and/or in several variables.
- Theory of Distributions: Convolution products and their usage.
- Laplace Transforms: The Operational Calculus of Oliver Heaviside.
- Integrability of a function and of its absolute value.
- Analytic functions of a linear operator. Defining f (D) when D is d/dx.
- Generalizing the Cauchy-Schlömilch substitution (for definite integrals).
- Feynman's trick: Put a parameter in the integrand and differentiate along it.
- Malmsten integrals: Tough family involving Log Log x (Malmsten, 1842).
- Ordinary differential equations. Several examples.
- A singular change of variable may not be valid over a maximal domain.
- Vertical fall against fluid resistance (valid for viscous and quadratic drag).
- Jet propulsion: Expelling stuff at speed u makes (u-v) m remain constant.
- Riccati equation: When y' is a quadratic function of y...
- Sturm-Liouville problem has nontrivial solutions only for some parameters.
- Frobenius method to solve a second-order differential equation.
- Fuchsian conditions for the applicability of the method of Frobenius.
- Differential forms and partial derivatives.
- Generalizing the fundamental theorem of calculus.
- Vectorial surface dotted into an observing direction gives apparent area.
- Practical identities of vector calculus.
Optimization: Operations Research, Calculus of Variations
- Stationary points (saddlepoints) are where all partial derivatives vanish.
- Classical optimizations: Heron's problem, Dido's problem, etc.
- Single-variable optimization: Derivative vanishes at any interior extremum.
- The angle maximization problem of Regiomontanus. Historical case study.
- Extrema of a function of two variables obey a second-order inequality.
- Saddlepoints of a multivariate function. One equation for each variable.
- Lagrange multipliers: Constrained optimization of an objective function.
- Minimizing the lateral surface area of a cone of given base and volume.
- Euler-Lagrange equations hold along the path of a stationary integral.
- Noether's theorem: One conserved quantity for each Lagrangian symmetry.
- Geodesics in a 2-dimensional surface are curves of least length.
- The brachistochrone curve is a cycloid (in a uniform gravitational field).
- Dido's problem. A geometric solution to the oldest variational problem.
- Isoperimetric Inequality: The largest area enclosed by a loop of unit length.
- Plateau extended the calculus of variations from paths to membranes.
- Embedded minimal surfaces: Plane, catenoid, helicoid, Costa's surface, etc.
- Connecting blue dots to red dots in the plane, without any crossings...
- Torricelli points and the shortest way to connect three guven dots.
- The Honeycomb Theorem: A conjecture of old, proved by Thomas Hales.
- Symmetrical monkey saddles of zero mean curvature.
- Counterexamples to Kelvin's conjecture. Unit spatial tiles of least area.
- J.J. Thomson's problem: N repelling charges on a spherical surface.
- Monge-Kantorovich optimal transport problem.
- Cauchy sequences help define real numbers rigorously.
- Borderline convergence. Prototypes of series which are barely convergent.
- A simple proof of convergence. Part of the mathematical folklore.
- Permuting the terms of a series may change its sum arbitrarily.
- Two decreasing divergent series may have a convergent minimum!
- Uniform convergence of continuous functions makes the limit continuous.


- Defining integrals: Cauchy, Riemann, Darboux...
- Lebesgue integrals. Horizontal slices, not vertical ones !
- Cauchy principal value of an integral.
- Fourier series. A simple example.
- Infinite sums evaluated with Fourier series.
- A double sum is often the product of two sums (possibly Fourier series).
- At a jump, a Fourier series is the half-sum of its left and right limits.
- Gibbs phenomenon; 9% overshoot of partial Fourier series near a jump.
- Method of Frobenius about a regular singularity of a differential equation.
- Laurent series of a function about one of its poles.
- Cauchy's Residue Theorem is helpful to compute difficult definite integrals.
- Tame complex functions: Holomorphic and meromorphic functions.
- Cauchy-Riemann equations. Also known as d'Alembert-Euler conditions.
- Wirtinger derivatives. Calculus methods for several complex variables.
- Cauchy integral formula. Fundamental theorem of complex analysis.
- Argument principle. The logarithmic integral counts zeros ans poles.
- Rouché's theorem: Nearby holomorphic functions have nearby zeros.
- Riemann mapping theorem and biholomorphic functions.
- Univalent functions (analytic injections) have nonvanishing derivatives.
- Schlicht functions are normalized analytic injections from the unit disk.
- Starlike schlicht functions & Bieberbach's conjecture restricted to these.
- Maximum-modulus principle: No local maxima for holomorphic functions.
- Epsilon-Delta. Elementary concept of a limit in a metric space.
- A function sandwiched between two functions of limit L has limit L.
- L'Hospital's rule on the limit of the ratio of two vanishing quantities.
- Taylor's expansion of a differentiable function as a power series.
- The remainder of a Taylor expansion can be expressed in several ways.
- Lagrange used Taylor's expansion to redefine Calculus algebraically.
- Radius of convergence. The convergence disk of a complex power series.
- Stolz sector: Slice of the disk of convergence with its apex on the boundary.
- Composition of two (formal) power series.
- Lagrange inversion formula and Lagrange-Bürmann inversion formula.
- The exponential series. Proving that exp (x) exp (y) = exp (x+y)
- Analytic continuation: Power series that converge on overlapping disks.
- Decimated power series are equal to finite sums involving roots of unity.
- Splitting a power series into its k classes of indices modulo k.
- Calculus of finite differences. Analog of calculus for discrete sequences.
- Fundamentals of asymptotics. The simple definition of a powerful tool.
- The big O notation is named after
Paul Bachman and Edmund Landau.
- Solving aymptotic equations. Method of dominant balance.
- Asymptotic expansions about a limit point may or may not converge.
- Moments, Stieltjes functions and Stieltjes series.
- Extracting information from an asymptotic series.
- Stirling's approximation and Stirling's series.
- Hyper-asymptotics: Aymptotics beyond all orders.
- Stokes phenomenon: Wedge where an asymptotic approximation is valid.
- WKB method: Asymptotic order-reduction of a linear differential equation.
- Summing geometric series: Equating things that match over some domain.
- Definitions and notations. Distinguishing a formal series from its sum.
- Desirable properties of summation methods yield rules for handling them.
- Stability of geometric series is often just assumed.
- All series with vanishing terms are stable, under any linear summation.
- Cauchy product of two series. It's a stable series if at least one factor is.
- Dirichlet convolution: Is the sum of a product the product of the sums?
- Infinite products: Exponentials of infinite series.
- Double summation. Series whose terms are themselves sums of series.
- Original Bernoulli numbers. Generated by z / (1-exp(-z)). So, B1 = ½.
- Formal series are kets. Linear summation methods are bras.
- Summation by convergence is compatible with regular summations.
- Functional analysis: Using the Hahn-Banach extension theorem.
- Euler summation (1746).
- Cesàro summations (1890).
- Borel summation (1899).
- Nørlund summations All are linear, regular and consistent (1919).
- Abel summation .
- Lindelöf summation (1903).
- Mittag-Leffler summation method (1908).
- Valiron summability (1917).
- Generalized summation methods, using arbitrary convergence factors.
- When does a series have a stable sum? Stability theorems.
- Weierstrass summation: Summation by analytic continuation (1842).
- Resummation with Meijer G-functions.
- Zeta-function regularization (1916). Dubbed heat-kernel regularization.
- Wonders of unstable summations. Linear summations of unstable series.
- Decimated power series can be worked out for divergent series too.
- Stretching a series doesn't change its sum, except when it does...
- Invariants of a series and the series of the sums of its decimations.
- Divergent Fourier series. An example of a stretched divergent series.
- Parametrized differential equations and their solutions as asymptotic series.
- The Mercator series is the integral of the geometric series (1668).
- Decimating the harmonic series, by taming a multivalued continuation.
- Sum of the harmonic series: ln 2p = 1.83787706640934548356065947...
- Darboux's summation formula generalizes the Euler-Maclaurin formula.
- Ramanujan's irregular summation (1913).
- Summations of p-adic integers for a special radix or for all of them.
- Moments, Stieltjes functions and Stieltjes series.
- Shanks' transformation greatly accelerates an alternating convergence.
- Richardson extrapolation.
- Index-free acceleration of sequences with harmonic convergence.
- Parametrized acceleration based on the expected type of convergence.
- Padé approximant. Simplest
rational function of given Taylor expansion.
- Compensated derivatives. In any ring or power-associative algebra.
- Wallis product (1655) due to John Wallis (1616-1703).
- Euler's product formula for sine, using the normalized sinc function.
- Factorization of the reciprocal Gamma function by Karl Weierstrass.
- Weierstrass factorization theorem (1876).
- Euler's partial-fraction expansion of the cotangent function.
- Mittag-Leffler's theorem (1876).
- Well-known pole expansions of a few meromorphic functions.
- Euler's formulas extract a harmonic component from a trigonometric sum.
- Fourier expansion of a function: The sum of all its harmonic components.
- Dirichlet's conditions are sufficient for a Fourier expansion to converge.
- Divergent Fourier expansion of the tangent function.
- Cantor's proofs of unicity and the introduction of U-sets.
- Simples rectangular waves. From periodic pulses to square waves.
- Sawtooth functions can be obtained by integration of rectangular waves.
- Clipped sinusoids. The harmonic distortion introduced by hard clipping.
- The direct product of two functions is a function of two variables.
- Convolution as an inner operation among numerical functions.

- Duality: The product of a bra by a ket is a (complex) scalar.
- A distribution associates a scalar to every test function.
- Schwartz functions are smooth rapidly decreasing test functions.
- Tempered distributions are continuous functionals over Schwartz functions.
- The Fourier Transform associates a tempered distribution to another.
- Competing definitions of the Fourier transform. For the record.
- Parseval's theorem (1799). The Fourier transform is unitary.
- Noteworthy distributions and their Fourier transforms:

- Dirac's d and the uniform distribution ( f (x) = 1).
- The signum function sgn(x) and its transform: i / ps
- The Heaviside step function H(x) = ½ (1+sgn(x)) and its transform.
- The square function P(x) = H(x+½)-H(x-½)
and sinc ( ps )
- The triangle function L(x) and
sinc2 ( ps )
- The normalized Gaussian distribution is its own Fourier transform.
- Central Limit Theorem (CLT).
- Far image of a picture on translucent film is its Fourier transform.
- Sampling formula: The unit comb
(
 ) is its own Fourier transform. ) is its own Fourier transform.
- Crystallography using X-ray diffraction (Max von Laue, Nobel 1914).
- Spectrum: Support of the Fourier transform.
- Quasicrystals: Distributions with a discrete support and a discrete spectrum.
- The Radon transform (used in lateral tomography) is easily inverted.
- Discrete Fourier Transform, defined as a unitary involution.
- Discrete Cosine Transform. JPEG lossy compression.
- The logic of Aristotle. Syllogisms about categorical propositions.
- The Barber's Dilemma is not a paradox, if analyzed properly.
- What is infinity? There's more to it than a pretty symbol (¥).
- Peano's axioms provide a rigorous definition of the set of natural integers.
- Ordered numbers: From integers to rational, real and surreal numbers.
- There are more real than rational numbers. Cantor's diagonal argument.
- Cantor's ternary set. A vanishing set of reals equipollent to the whole line.
- The language of set theory: Symbols and idioms useful to anybody.
- The axioms of set theory: Basic ZF axioms (without any choice principle).
- The Axiom of choice (AC) is the most powerful choice principle (ZFC).
- The Axiom of restriction isn't needed in ZFC set theory (AC implies it).
- Equivalents and lesser alternatives to the Axiom of choice.
- The existence of nonmeasurable sets is guaranteed by the Axiom of choice.
- Should we drop the Axiom of choice ?
- Binary cartesian products. Multiple cartesian products. Infinite ones.
- Binary relations between two sets are subsets of their cartesian product.
- Functions and applications are special types of binary relations.
- A set is smaller than its powerset: A simple proof applies to all sets.
- Transfinite cardinals describe the various sizes of infinite sets.
- The continuum hypothesis: Is the continuum the smallest uncountable set?
- Transfinite ordinals: Counting to infinity... and beyond.
- Hartogs number of a set (well-ordered or not). A well-defined ordinal.
- Surreal numbers include reals, transfinite ordinals, infinitesimals & more.
- Multidimensional (hypercomplex) numbers: To octonions and beyond.
- Naming hypercomplex numbers beyond sedenions.
- Power associativity: What multiplication needs to allow exponentiation.
- A set belongs to a class in NBG (a conservative extension of ZFC).
- Tarski-Grothendieck theory (TG) is a nonconservative extension of ZFC.
- Categories: History, motivation, definition. Objects & morphisms.
- Initial objects and final objects. A zero object is both initial and final.
- Finite categories.
- Set : Category of sets and functions.
- Rel : Category of sets and relations.
- Example of categories: Large or small, abstract or concrete.
- Constructing new categories from pre-existing ones.
- Functors are homomorphisms between categories.
- Cat : Category of small categories and functors.
- Natural transformations are morphisms in a category of functors (1942).
- Duality. The opposite of a category is obtained by reversing all arrows.
- Isomorphisms in a category are reversible morphisms (arrows) in it.
- Groupoid: Small category in which all morphisms are reversible.
- The product of two objects, if defined, is an equivalence class of objects.
- Exponential of two objects. Counterpart of function spaces for sets.
- Cartesian-closed categories (CCC). Well-defined products & exponentials.
- Yoneda lemma and Yoneda embedding.
- Adjoint functors.
- Monads.
- Abelian categories.
- Regular categories.
- Exact categories.
- Exact sequences of morphisms. The image of one is the kernel of the next.
- Homologies and cohomologies. How sequences fail to be exact.
- Should categories replace sets at the foundation of all mathematics?
- Categorial quantum mechanics. Describing physics with category theory.
Topos (Category Theory)
- Presheaves and sheaves.
- Bohr topos.
- Elementary topos (Lawvere).
- Grothendieck topos.
- Kochen-Specker theorem. Categorial expression of quantum theory.
- Von Neumann's algebras.
- Connes-Consani plane connection.
- The number 1 is not prime. Good definitions allow simple theorems.
- Composite numbers aren't prime, but the converse need not be true...
- Two prime numbers whose sum is equal to their product.
- Gaussian integers: Factoring into primes on a two-dimensional grid.
- The least common multiple, obtained without factoring into primes.
- Standard factorizations: n4 + 4 is never prime for
n > 1 because...
- High-order Aurifeuillian factorizations using polynomial identities.
- Euclid's algorithm gives the GCD and the related Bézout coefficients.
- Bézout's Lemma: The GCD of p and q is of the form u p + v q.
- Greatest Common Divisor (GCD) defined for all commensurable numbers.
- Linear equation in integers can be solved using Bézout's lemma.
- Pythagorean Triples: Right triangles whose sides are coprime integers.
- The number of divisors of an integer.
- Perfect squares are the only integers with an odd number of divisors.
- The product of all divisors is often a perfect square.
- Even perfect numbers are well-known. Are there any odd ones out there?
- Mersenne primes are the odd parts of the even perfect numbers.
- Multiperfect & hemiperfect numbers. Whole or half-integral abundancies.
- Fast exponentiation by repeated squaring.
- Partition function. How many collections of positive integers add up to 15?
- A Lucas sequence whose oscillations never carry it back to -1.
- A bit sequence with intriguing statistics. Counting squares between cubes.
- Binet's formulas: N-th term of a sequence obeying a linear recurrence.
- The square of a Fibonacci number is almost the product of its neighbors.
- D'Ocagne's identity relates conjugates products of Fibonacci numbers.
- Catalans's identity generalizes Cassini's Identity.
- Faulhaber's formula gives the sum of the p-th powers of the first n integers.
- Multiplicative functions: If a and b are coprime, then
f (ab) = f (a) f (b).
- Moebius function: Getting N values with O(N Log(Log N)) additions.
- Dirichlet convolution is especially interesting for multiplicative functions.
- Fractional Dirichlet powers of arithmetic functions with positive lead.
- Dirichlet powers of the Möbius function and/or its inverse u = 1,1,1,1,1...
- Convolutive subgroup generated by u = 1,1,1,1,1... and N = 1,2,3,4,5...
- Dirichlet powers of multiplicative functions are given by a superb formula.
- Totally multiplicative functions are the simplest multiplicative functions.
- Dirichlet characters are important totally multiplicative functions.
- Euler products for L-functions. Generalized Riemann hypothesis.
- Logarithms of L-functions. Sums of series indexed by the prime powers.
- Expressing L-functions in term of Hurwitz zeta functions and vice-versa.
- Additive functions: If a and b are coprime, then
f (ab) = f (a) + f (b).
Cryptography: Ciphers and Codebreaking
- Simple shift ciphers: Caesar's cipher, Augustus cipher. ROT13.
- Substitution cipher.
- Tranposition ciphers. Tri-code.
- Disk ciphers.
- The Vigenère cipher can be broken with the Babbage-Kasisky method.
- Bazeries cylinders consist of many stacked coding disks (Jefferson, 1795).
- Rotor machines were invented in 1915 and still used in the 1980s.
- The German Enigma. Broken by Marian Rejewski and Alan Turing.
- Backdoor in elliptic curve cryptography. NSA surveillance controversy.
- The Voynich manuscript (c. 1420): The book that nobody could read.
Modularity: Elliptic curves and modular forms
- Fermat's Last Theorem (FLT) is a consequence of the modularity theorem.
- Elliptic functions are doubly-periodic functions of a complex variable.
- Elliptic curves: Nonsingular cubics in the projective plane.
- Modular forms.
- Modularity theorem: Every elliptic curve is modular.
- Ramanujan's Tau Function and the Sato-Tate conjecture (proved in 2011).
- Modular arithmetic can tell the last digits of extremely large numbers.
- Leading digits of insanely large numbers can't be found by logarithms.
- Powers of ten expressed as products of two factors without zero digits.
- Divisibility by 7, 13, and 91 (or by B2-B+1 in base B).
- Lucky 7's. Any integer divides a number composed of only 7's and 0's.
- The decimal representation of rational numbers is ultimately periodic.
- Midy's theorem: Properties of periods in radix-B numeration.
- Numbers with two decimal expansions. E.g., 1 and 0.99999999999999...
- Binary and/or hexadecimal numeration for floating-point numbers as well.
- Extract a square root the old-fashioned way.
- Ternary system: Is base 3 really the best radix for positional numeration?
- Dozenal counting: (Roman) ounce, as, dozen, gross, great-gross.
- Sexagesimal numeration is still with us. Cuneiform writing isn't.
- Divisors can be defined in any additive semigroup.
- Relatively prime integers: The GCD of two coprime integers is 1.
- A prime number is a positive integer with 2 distinct divisors (1 and itself).
- Lemma: Every integer larger than 1 has at least one prime factor.
- Fundamental theorem of arithmetic. The factorization into primes is unique.
- Euclid's proof: There are infinitely many primes.
- Dirichlet's theorem: There are infinitely many primes of the form kN+a.
- Green-Tao theorem: Arbitrarily long arithmetic progressions of primes.
- Von Mangoldt's function is Log p for a power of a prime p, 0 otherwise.
- Prime Number Theorem: The probability that N is prime is roughly 1/ln(N).
- Riemann's power-prime counting function (J). Riemann's explicit formula.
- The average number of factors of a large number N is Log N.
- The average number of distinct prime factors of N is Log Log N.
- The largest known prime: Historical records, old and new.
- The Lucas-Lehmer Test checks the primality of a Mersenne number fast.
- Proth primes are almost as fast to check as Mersenne primes.
- Sierpinski numbers are moduli for which no Proth number is prime.
- Pratt primality certificates give quick automated proofs of primality.
- The AKS test determines the primality of any number in polynomial time.
- Formulas giving only primes may not help with new primes.
- Ulam's Lucky Numbers and other sequences generated by sieves.
- Chinese remainder theorem: Remainders define an integer, within limits.
- Modular arithmetic: The formal algebra of congruences, due to Gauss.
- Fermat's little theorem: For a prime p not dividing a,
ap-1 is 1 modulo p.
- Euler's totient function: f(n) counts the integers coprime to n, from 1 to n.
- Fermat-Euler theorem: If a is coprime to n,
a to the f(n) is 1 modulo n.
- Carmichael's reduced totient function (l) : A special divisor of the totient.
- 91 is a pseudoprime to half of the bases coprime to itself.
- Carmichael Numbers: An absolute pseudoprime n divides
an-a for any a.
- Chernik's Carmichael numbers: 3 prime factors (6k+1)(12k+1)(18k+1).
- Other products that yield a Carmichael number iff every factor is prime.
- Large Carmichael numbers may be obtained in various ways.
- Conjecture: Any odd integer coprime to its totient has Carmichael multiples.
- Monoids feature an associative operation and a neutral element.
- The inverse of an element comes in 2 flavors that coincide when both exist.
- Free monoid: All the finite strings (words) in a given alphabet.
- Raising something to the power of an integer.
- Groups are monoids in which every element is invertible.
- A subgroup is a group contained in another group.
- Ideals of a semigroup are subsemigroups.
- Generators of a group are not contained in any proper subgroup.
- Presentation of a group: A set of generators followed by relators.
- Lagrange's theorem: The order of a subgroup divides the order of the group.
- Cauchy's theorem: If a prime p divides |G|, some element of G has order p.
- Sylow's theorems. On the possible orders of subgroups of a finite group.
- Normal subgroups and their quotients in a group.
- Wielandt's symbol asserts that a set is a normal subgroup of a group.
- Homomorphism: The image of a product is the product of the images.
- The symmetric group on E consists of all the bijections of E onto itself.
- Inner automorphisms: Inn(G) is isomorphic to G modulo its center.
- Outer automorphism group: The automorphisms of G modulo Inn(G).
- Complete groups (unrelated to completeness in metric or uniform spaces).
- The conjugacy class formula uses conjugacy to tally elements of a group.
- Simple groups are groups without nontrivial normal subgroups.
- The derived subgroup of a group is generated by its commutators.
- Direct product of two groups (called a direct sum for additive groups).
- Finite abelian groups are either cyclic or direct sums of cyclic groups.
- Holomorph of G : The canonical semi-direct product of G and Aut(G).
- Groups of small orders. Basic families: Cyclic groups, dihedral groups, etc.
- Q8: The quaternion group. Quaternion numbers (Hamilton, 1843).
- The gamma group of order 32 is generated by Dirac's 4 gamma matrices.
- D4: An incomplete group of order 8, isomorphic to its automorphisms.
- Enumeration of small groups. How many groups of order n?
- Classification of finite simple groups, by Gorenstein and many others.
- Sporadic groups: Tits Group, 20 relatives of Fischer's Monster, 6 pariahs.
- Torsion of a group: The set of all elements whose orders are finite.
- Linear representations are homomorphisms into a group of matrices.
- Classical groups: Their elements depend on parameters from a field.
- Projective qualifier may denote a group modulo its own center.
- The Möbius group consists of homographic transformations of
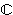 È{¥}. È{¥}.
- The modular group G
is the projective special linear group PSL(2,
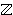 ). ).
- Group structure of an elliptic curve.
- Degenerate elliptic curve consisting of a circle and a straight line.
- Amenable groups are locally compact topological groups allowing a mean.
- The Chameleon Groups (F, T and V) of Richard J. Thompson (1965).
- Abelian sandpile groups. The neutral element is not immediately obvious.
- Lorentz transformations may change spatial orientation or time direction.
- Symmetries of the laws of nature: A short primer.
- The renormalization group is a subgroup of the cosmic Galois group.
Ring Theory: Commutative & Noncommutative Rings
- A Brief History of Rings.
- Rings are sets endowed with addition, subtraction and multiplication.
- Divisors of zero include all nilpotents. Zero-divisors
(if any) are nonzero.
- Units are invertible elements. That's also meaningful in non-unital rings.
- Ideals within a ring are multiplicatively absorbent additive subgroups.
- Quotient ring, modulo an ideal: The residue classes modulo that ideal.
- Ring homomorphisms and isomorphisms. All kernels are ideals.
- Nonzero characteristic: Least n for which all sums of n like terms vanish.
- The SUN ring has 8 elements. Smallest unital noncommutative ring.
- Idempotent elements allow the Peirce decomposition of a ring.
- Finite rings. Smallest examples, enumeration and classification.
- Simple rings. A simple ring has only two ideals; {0} and itself.
- Coprime ideals and generalized Chinese remainder theorem.
- Bezout rings: Rings where the sum of two principal ideals is principal.
- Primary ideals are to ideals what prime-powers are to integers.
- Cauchy multiplication is well-defined for formal power series over a ring.
- Ring of univariate polynomials A[X] with coefficients in a given ring A.
- Noetherian rings don't have any infinite ascending chain of ideals (ACC).
- Artinian ring: Noetherian with every element either invertible or nilpotent.
- Lasker-Noether theorem. Generalized fundamental theorem of arithmetic.
- Greatest common divisor (GCD) always exists for a pair in a GCD domain.
- Factorial domain (UFD). GCD domain with ACC for principal ideals.
- Galois rings. Residues of modular polynomials, modulo one of them.
- Hilbert rings, where every prime ideal is an intersection of primitive ideals.
- Abelian rings are rings where every idempotent element is central.
- Commutative local rings and their modules: Local algebra (1938).
- Topological rings Both operators are continuous.
- Involutive rings are endowed with an involutive anti-automorphism.
- Etale homomorphisms of rings.
- Morita equivalence (on rings).
- Vocabulary: We consider skew fields to be noncommutative. Some don't.
- Fields are commutative rings where all nonzero elements are invertible.
- Quotient field of a ring without divisors of zero.
- Wedderburn's Theorem: Finite division rings are necessarily commutative.
- Every finite integral domain is a field.
- Galois fields are the finite fields. Their orders are powers of primes.
- Polynomials in a Galois field. Irreducible and primitive polynomials.
- The trivial field is a singleton. It's the only field where 0 is invertible.
- Splitting field of P in F[x] : Smallest extension of F where P fully factors.
- Perfect fields include fields of characteristic zero and all finite fields.
- The field of Laurent series.
- Conway's Nim-Field is algebraically complete. It contains infinite ordinals.
- Ternary multiplication compatible with ternary addition (without "carry").
- Vectors were originally just differences between points in ordinary space...
- Abstract vector spaces: Vectors can be added, subtracted and scaled.
- Dimension of a vector space: The number of its independent generators.
- Subspaces. Intersection. Sum. Direct sums of supplementary subspaces.
- Linear maps between vector spaces respect addition and scaling.
- Quotient of two vector spaces. Hyperplanes have codimension 1.
- Fundamental theorem of linear algebra and rank theorem.
- Normed vector spaces. The fundamental properties of a norm.
- Inner-product spaces over the field of complex numbers.
- Dual space: The set of all [continuous] linear functions with scalar values.
- Lebesgue spaces. Sequence spaces exemplify more general types.
- Tensors: Multilinear functions of vectors and covectors with scalar values.
- Graded linear spaces are direct sums of homogeneous spaces.
- Algebra: A vector space with a scalable and distributive internal product.
- Lie algebra: Anticommutative algebra obeying Jacobi's identity.
- Jordan algebra: Commutative and alternative algebras (Jordan, 1933).
- Albert algebra: Exceptional 27-dimensional Jordan-algebra (Albert, 1934).
- Clifford algebra: Unital associative algebra endowed with a quadratic form.
- Dual numbers with a second component squaring to zero (Clifford, 1873).
- Spacetime algebra: Cl(1,3) is the Clifford algebra with Minkowski metric.
- Things that are not vectorial because they're not defined intrinsically.
- David Hestenes proposed geometric calculus as a denotational unification.
- Modules are vectorial structures over a ring of scalars (instead of a field).
- Free modules have a basis similar to that of vector spaces.
- Injective modules. The rationals form an injective module over the integers.
- Projective modules. Due to Eilenberg & Cartan (1956).
- Flat modules. Devised by Jean-Pierre Serre in 1956.
- Definition of a tensor.
- Metric spaces: Linking contravariant and covariant representations.
- Gradient: Tensor of rank 1 in covariant form.
- Convex sets in a real vector space.
- Real-valued convex functions of a vectorial variable.
- Uniformly convex spaces.
- Aspect ratio: The length divided by the height (i.e., the smallest width).
- A norm is characterized by a closed convex body, symmetric about 0.
- Convex hull: Conv (S) is the smallest convex set containing the set S.
- Closed halfspaces generate all closed convex sets by intersection.
- Polar of a closed convex set. Dot-product duality among convex bodies.
- Separating hyperplane (in the loose sense) between disjoint convex sets.
- A compact convex can be strictly separated from a disjoint closed convex.
- Two disjoint open convexes are separated by a nonintersecting hyperplane.
- Functionals assign scalar values to some functions over an infinite set I.
- Topological vector spaces. Banach spaces are normed and complete.
- Eduard Helluy (1912): The space C[a,b] (continuous functions over [a,b]).
- Sublinear functionals are merely subadditive and positively homogeneous.
- Hahn-Banach extension theorem. Extending a dominated linear functional.
- Hahn-Banach separation theorem. A different view of the same result.
- Generalization of Hahn-Banach to complex or quaternionic linear spaces.
- The two Baire category theorems (1899).
- Uniform boundedness principle. The Banach-Steinhaus theorem.
- Open mapping theorem. The Banach-Schauder theorem.
- Weak convergence and weak* convergence.
- Banach-Alaoglu theorem (1940).
- Krein-Milman theorem: Retrieving a compact convex set from its extremes.
- Nuclear spaces cover practical cases besides Banach spaces.
- Nuclear operators.
- Compact operators.
- Schauder basis.
- The ring of p-adic integers. Objects with infinitely many radix-p digits.
- Polyadic integers: Greek naming of p-adic integers.
- What if p isn't prime? Dealing with zero-divisors.
- Decadic integers: The strange realm of 10-adic integers (composite radix).
- Decadic puzzle: A tribute to the columnist J.A.H. Hunter (1902-1986).
- The field of p-adic numbers. Quotient field of the ring of p-adic integers.
- Dividing two p-adic numbers looks like long division, only backwards...
- Overbar notation, for p-adic and rational numbers alike.
- The p-adic metric can be used to define p-adic numbers analytically.
- The reciprocal of a p-adic number computed by successive approximations.
- Ratios of rational integers have two representations: g-adic and radix-g.
- Solving algebraic equations in p-adic integers.
 -linear maps between -linear maps between
 and Qp are discontinuous at every point. and Qp are discontinuous at every point.
- Hasse's local-global principle. Established for the quadratic case in 1920.
- Rotating digit patterns (in base g) may double the corresponding values.
- Rotating digits one place to the left divides some integers by k.
- Ordinary fractions added with Nim rules.
- Multiplicatiion of ordinary fractions added with Nim rules.
- Nim square-root.
- Pseudoprimes to base a. Poulet numbers are pseudoprimes to base 2.
- Weak pseudoprimes to base a : Composite integers n dividing
(an-a).
- Counting the bases to which a given composite number is a pseudoprime.
- Strong pseudoprimes to base a are less common than Euler pseudoprimes.
- The witnesses of a composite number: At least 75% of nontrivial bases.
- Rabin-Miller Test: An efficient and trustworthy stochastic primality test.
- The product of 3 primes is a pseudoprime when all pairwise products are.
- Super-pseudoprimes: All their composite divisors are pseudoprimes.
- Maximal super-pseudoprimes have no super-pseudoprime multiples.
- Wieferich primes are scarce but there ought to be infinitely many of them.
- Jevons Number. Factoring 8616460799 is now an easy task.
- Challenges help tell special-purpose and general-purpose methods apart.
- Special cases of a priori factorizations are helpful to number theorists.
- Trial division may be used to weed out the small prime factors of a number.
- Ruling out factors can speed up trial divison in special cases.
- Pocklington's lemma: Conditions imposing the form of unknown factors.
- Recursively-defined sequences (over a finite set) are ultimately periodic.
- Pollard's rho factoring method is based on ultimately periodic sequences.
- Pollard's p-1 Method finds prime factors p for which p-1 is smooth.
- Williams' p+1 Method is based on the properties of Lucas sequences.
- Lenstra's Elliptic Curve Method generalizes Pollard's p-1 approach.
- Dixon's method: Combine small square residues into a solution of
x 2 º y 2
- Shors's algorithm would work in polynomial time on a quantum computer.
- Motivation: On the prime factors of some quadratic forms...
- Quadratic residues: Half of the nonzero residues modulo an odd prime p.
- Euler's criterion: A quadratic residue raised to the power of (p-1)/2 is 1.
- The Legendre symbol (a|p) extends to values of p besides odd primes.
- The law of quadratic reciprocity states a simple but surprising fact.
- Gauss' Lemma expresses a Legendre symbol as a product of many signs.
- Eisenstein's Lemma: A variation of Gauss's lemma allows a simpler proof.
- One of many proofs of the law of quadratic reciprocity.
- Artin's Reciprocity.
- What is a continued fraction? Example: The expansion of p.
- The convergents of a number are its best rational approximations.
- Large partial quotients allow very precise approximations.
- Regular patterns in the continued fractions of some irrational numbers.
- In almost all cases, partial quotients are ≥ k with probability lg(1+1/k).
- Elementary operations on continued fractions.
- The Baire space: Continued fraction expansions of irrationals in [0,1].
- Expanding functions as continued fractions.
- Expanding functions as continued exponentials.
- Engel expansions of positive numbers are nondecreasing integer sequences.
- Pierce expansions of numbers from 0 to 1. Strictly increasing sequences.
- Continued fractions in the complex realm. Algorithm of Asmus L. Schmidt.
- Counterfeit Coin: In 3 weighings, find an odd object among 12, 13 or 14.
- Counterfeit Penny Problem: Find an odd object in the fewest weighings.
- Seven-Eleven: Four prices with a sum and product both equal to 7.11.
- Equating a right angle and an obtuse angle, with a clever false proof.
- Choosing a raise: Trust common sense, beware of fallacious accounting.
- 3 men pay $30 for a $25 hotel room, the bellhop keeps $2... Is $1 missing?
- Chameleons: A situation is unreachable because of an invariant quantity.
- Sam Loyd's 14-15 puzzle also involves an invariant quantity (and 2 orbits).
- Einstein's riddle: 5 distinct colors, nationalities, drinks, smokes and pets.
- Numbering n pages of a book takes this many digits (formula).
- The Ferry Boat Problem (by Sam Loyd): To be or not to be ingenious ?
- Hat overboard ! What's the speed of the river?
- All digits once and only once: 48 possible sums (or 22 products).
- 2-people bridge crossed by 4 people (U2). Four paces, one flashlight!
- Managing supplies to travel 6 days while carrying enough for only 4 days.
- Go south, east, north and you're back... not necessarily to the North Pole!
- Icosapolis: Put 1 to 20 in a 5 by 4 grid so neighbors differ by at least 4.
- Unusual mathematical boast for people born in 1806, 1892, or 1980.
- Puzzles for extra credit: From Chinese remainders to bookworms.
- Simple geometrical dissection: A proof of the Pythagorean theorem.
- Early bird saves time by walking to meet incoming chauffeur.
- Sharing a meal: A man has 2 loaves, the other has 3, a stranger has 5 coins.
- Fork in the road: Find the way to Heaven by asking only one question.
- Proverbial Numbers: Words commonly associated with some numbers.
- Riddles: The Riddle of the Sphinx and other classics, old and new.
- Crossing the Panama Canal east to west to reach the Pacific Ocean.
- Martin Gardner (1914-2010) described himself as "strictly a journalist".
- Flexagons: Hexaflexagons were popularized by Martin Gardner in 1956.
- Polyominoes: The 12 pentominoes and other tiles invented by Sol Golomb.
- Soma: 7 nonconvex solids consisting of 3 or 4 cubes make a larger cube.
- Tessellations by convex pentagons. The contributions of Marjorie Rice.
- Kites and Darts. The aperiodic tilings of Roger Penrose.
- Ambigrams: Calligraphic spellings which change when rotated or flipped.
- The Game of Life. John Conway's endearing cellular automaton (1970).
- Rubik's Cube: Ernõ Rubik (1974) Singmaster (1979) Gardner (1981).
- It's impossible to tie a knot without letting go of the ends of the string.
- On the limited knowledge of Man. An Indian legend...
- 1089: Subtract a 3-digit number and its reverse, then...
- Multiples of Nine: A secret symbol is revealed.
- Casting Out Nines: A missing digit is revealed.
- Triple threat mind reading.
- Mass media mentalism by David Copperfield (1992).
- Grey Elephants in Denmark: Classroom mental magic.
- Fitch Cheney's 5-card trick: 4 cards tell the fifth one.
- Generalizing the 5-card trick and Devil's Poker...
- Kruskal's Count.
- Paths to God.
- Stacked Deck.
- Enigma Card Trick.
- Magic Age Cards.
- Ternary Cards.
- Magical 21 (or 27).
- The Final 3 are the chosen cards.
- Boolean Magic.
- Perfect Faro Shuffles.
- Relocate the top card to any given position using at most 7 faro shuffles.
- Equal Numbers of Heads !
- Gilbreath principle: Predictability survives a riffle-shuffle (1958, 1966).
- Divination by counting. A self-working trick by Paul A. Lelikis (c. 1970).
- Last card: Tell the last card after being shown all the others.
- Deceit and lying.
- Misdirection.
- Find the Lady.
- Cups and balls. One of the most ancient tricks.
- Chop cup. Invented by "Chop-Chop" Wheatley in 1954.
- Invisible Thread Reel (ITR) by James George (1992).
- Force and Reveal: A whole class of magic tricks.
- Bill Simon's Prophecy Move (1952).
- Dots and Boxes: The "Boxer's Puzzle" position of Sam Loyd.
- The Game of Nim: Remove items from one of several rows. Don't play last.
- Sprague-Grundy numbers are defined for all positions in impartial games.
- Moore's Nim: Remove something from at most (b-1) rows. Play last.
- Normal Kayles: Knocking down a pin or two adjacent pins may split a row.
- Grundy's Game: Split a row into two unequal rows, if at all possible.
- Wythoff's Game: Take either from one heap or equally from both heaps.
- Origins of Chess: Chaturanga (India) & Shatranj (Persia). 7th century.
- Chess boards. Tables, boards and mats.
- Chess men. Styles and sizes of chess pieces. Weighted or magnetized.
- Wood and other materials for chessmen and chessboards.
- Time controls. Use of modern chess clocks for tournament-like play.
- Chess bag to hold full-sized chessmen, a clock and a rolled-up mat.
- Chess notation. Squares: a1 to h8. Pieces: K, Q, R, B and N.
- Openings: Structured list of common opening lines (names & links).
- Combinatorics of chess.
- Single-byte encoding of most half-moves in chess, with rare extra byte.
- Systems of play: Desired configurations of several pieces.
- Chess maxims: Guiding principles in the form of Proverbs.
- Textbook endgames: Foolproof recipes for some well-known endgames.
- Nalimov Tables: Perfect computerized analysis of endgame situations.
- Evaluation function: Estimating a quiescent position statically.
- Minimax search tree: The basic paradigm for analyzing two-player games.
- Alpha-beta pruning. In a minimax search, some alternatives can be ignored.
- Hash tables. How to avoid analyzing the same position more than once.
- Shortest chess games. Checkmates occurring during the opening moves.
- Mate in N moves.. The quintessential type of chess puzzles.
- Traxler's Counterattack. Analyzing a wild strategy against the fried-liver.
- Miniature games, including the Immortal Game of 23 moves.
- Classic traps: Fishing pole, etc.
- Elo ratings: Idealized probabilities and actual frequencies.
- Odds Chess: The old-fashioned handicapping system.
- Over-the-board chess titles from FIDE or national federations.
- Leading chess centers and famous chess venues, throughtout History.
- World champions. Historical dominance and formal championships.
- Glossary of common chess terms, classified by topic.
- A brief history of Go.
- The board (standard goban). 361 intersections of lines in a 19 by 19 grid.
- 361 stones. 181 black pieces and 180 white ones (usually lenticular).
- Go bowls (gosu). Japanese wooden bowls. Baskets from China.
Rules of the Game of Go :
- Komi: Points received by White as compensation for starting second.
- Score = (surrounded territory) + (captured stones) + komi.
- Liberty: A chain of stones is captured when all its liberties vanish.
- Rules of ko: Japanese and Chinese rules differ in the rare case of triple ko.
- Playing Go on unusual boards. Big or small, rectangular or not...

- Combinatorics of Go. Enumerating legal Go configurations.
- Nalimov tables. How Go has been solved for small grids.
Playing Go. Concepts, Tactics and Strategy :
- Opening moves (fuseki). What to play first (and why).
- Mistakes to avoid. What not to do and why not to do it.
- Shapes: Some localized patterns which skilled players are all familiar with.
- Ladders and loose ladders. Repeatedly prevent increase in opponent's air.
- Nets. Loose limits which make captures inescapable. Elementary reading.
- Snapback. A sacrifice may allow a greater capture in return.
- Eyes and eye-shapes are the keys to life-and-death problems.
- Seki. Shared life. Configurations that would backfire if you touch them.
- Tesuji. Finding key moves.
- Joseki. The Go term for a standard sequence of moves worth memorizing.
- Framework (moyo) to consolidate and/or defend against invasions.
- Invasions. Challenging the opponent's claim to a territory.
- Endgame. Squeezing the most of the situation when the end is near.
Go Players and the World of Go :
- Kyu (k) & dan (d). Pro dan or ping (p). Pecking order in Go.
- Competitions: Amateur and professional tournaments.
- Championships and champions: Past and present stars of the Go world.
- Machines that play Go. In March 2016, AlphaGo beat Lee Sedol, 9p.
- Go jargon: A short glossary of Go words indispensable in English.
- 4500-year history of the 20-square race game and its rosettes.
- Normal route and short lap: The two variants of the basic rules.
- Complex variants: Pieces are flipped for the second part of their routes.
- All variants ever played and then some. Classification and naming.
- Number of positions with n pieces per player.
- Traditional tetrahedral dice. Using 3 or 4 dice changes everything.
- Nalimov table for the single-lap Royal Game of Ur (7 pieces per player).
- Northwest Corner devised new rules for the Mesopotamian equipment.
- The pigeonhole principle: What's entailed by fewer holes than pigeons.
- Among 70 distinct integers between 1 and 200, two must differ by 4, 5 or 9.
- n+1 of the first 2n integers always include two which are coprime.
- Largest sets of small numbers with at most k pairwise coprime integers.
- Ramsey's Theorem: Monochromatic complete subgraphs of a large graph.
- Infinite alignment among infinitely many lattice points in the plane? Nope.
- Infinite alignment in a lattice sequence with bounded gaps? Almost...
- Large alignments in a lattice sequence with bounded gaps. Yeah!
- Van der Waerden's theorem: Long monochromatic arithmetic progressions.
- Happy-Ending problem: Unavoidable convex n-gons among m points.
- Unavoidable monochromatic Pythagorean triples with 2 colors in 1-7825.
Computer Science: Computability and Undecidability.
- Finite-state automata. The simplest type of computing machines.
- Deterministic and nondeterministic machines.
- Pushdown automata (PDA) recognize context-free languages (CFL).
- Two-way deterministic pushdown automata simulated in linear time.
- Turing-machines run a finite program on an infinite read-write tape.
- Universal Turing machine executes a program stored on its data tape.
- Almost all decision problems are not computable. The sad truth.
- The halting problem. Fundamental limitation of computers.
- The Ackermann function is total computable but not primitive recursive.
- The busy-beaver function (Radó's Sigma function) isn't computable.
- Church-Turing Thesis: If it can be done, a Turing machine can do it.
- Turmites. Langton's Ant and other two-dimensional Turing machines.
- Cellular automata (1D or 2D) can be Turing-complete.
Subreal Numbers: The field of computable numbers.
- Subreal numbers are computed by convergent two-tape Turing machines.
- Subreal numbers are countable because Turing machines are.
- The set of subreal numbers is not complete.
- Equality of subreal numbers isn't computable by any general procedure.
- Rational numbers are quotients of two integers.
- Some irrational numbers:
Surds. Logarithmic ratios of coprime integers.
- Constructible numbers can be constructed with straightedge and compass.
- Algebraic numbers are roots of polynomials with integer coefficients.
- Subreal numbers: Only countably many real numbers can be computed.
- Transcendental numbers. Almost all of them aren't even computable.
- Irrationality measure.
- Louville's (transcendental) numbers have infinite irrationality measure.
- Pickover's Flint Hills series. Governed by the
irrationality measure of p.
- Stable marriages: Two people shouldn't prefer each other to their spouses.
- Ford-Fulkerson algorithm. Best network flow from source to sink (1956).
- Heap priority queues allow sorting in O( n Log n ) worst time (1964).
- Alphabetic sorting is often not performed by pairwise comparisons.
- Radix sorting: Sorting n integers in linear time with radix-n numeration.
- Best path in a network: Dijkstra's algorithm and Bellman-Ford algorithm.
- " A* " best-first search uses a heuristical underestimate of the cost to a goal.
- Alpha-Beta Prunning Algorithm: Finding a minimax value in optimal time.
- String-matching in sublinear time. The Knuth-Morris-Pratt algorithm.
- Union-find: Linked partitions allow component merging and fast retrievals.
- Dynamic programming. Store partial results to avoid duplication of efforts.
- Minimum spanning tree. Least costly set of edges retaining connectivity.
- Linear programming in polynomial time. Foregoing the simplex algorithm.
- Ford circles: Kissing circles touching the real line at rational points.
- Farey series: The rationals from 0 to 1, with a bounded denominator.
- The Stern-Brocot tree features every positive rational once and only once.
- Eisenstein-Stern sequence (Calkin-Wilf tree) enumerates the rationals too!
- Any positive rational is a unique ratio of two consecutive Stern numbers.
- Pick's formula gives the area of a lattice polygon by counting lattice points.
History :
- Earliest mathematics on record. Before Thales was Euphorbus...
- Indian numeration became a positional system with the introduction of zero.
- Roman numerals are awkward for larger numbers. [ Unabridged version ]
- The invention of logarithms: Napier, Bürgi, Briggs, St-Vincent, Euler.
- The earliest mechanical calculators. W. Shickard (1623) & Pascal (1642).
- The Fahrenheit Scale: 100°F was meant to be the normal body temperature.
- The revolutionary innovations which brought about new civilizations.
Nomenclature & Etymology :
- The origin of the word algebra, and also that of algorithm.
- The name of the avoirdupois system is from a pristine form of French.
- Long Division: Cultural differences in long division layouts.
- Is a parallelogram a trapezoid? In a mathematical context, yes it is...
- Naming polygons. Greek only please; use hendecagon not "undecagon".
- Chemical nomenclature: Sequential names are systematic or traditional.
- Fractional prefixes: hemi (1/2)
sesqui (3/2) hemipenta (5/2) hemisesqui (3/4).
- Matches, phosphorus, and phosphorus sesquisulphide.
- Zillion. Naming large numbers.
- Zillionplex. Naming huge numbers.
- Abbreviations: Abbreviations of scholarly Latin expressions.
- "Resp." is a mathematical symbol whose syntax isn't that of respectively.
- Typography of long numbers.
- Intervals denoted with square brackets (outward for an excluded extremity).
- Dates in the simplest ISO 8601 form (with customary time stamps or not).
- The names of operands in common numerical operations.
- Spoken numbers.
- Pronouncing mathematical expressions, like native English speakers do.
- PEMDAS: A mnemonic for a rule that should not be taught.
- Physical units: Their products and their ratios.
- The heliocentric system was known two millenia before Copernicus.
- The assistants of Galileo and the mythical experiment at the Tower of Pisa.
- Switching calendars: Newton was not born the year Galileo died.
- The Lorenz Gauge is due to Ludwig Lorenz (1829-1891) not H.A. Lorentz.
- Special Relativity was first formulated by Henri Poincaré (1854-1912).
- Radioactivity was discovered in 1857, by Abel Niépce de Saint-Victor.
- The Fletcher-Millikan "oil-drop" experiment isn't entirely due to Millikan.
- Collected errata about customary physical units of measurement.
- Portrait of Legendre: The mathematician was confused with a politician.
- Incorrect depictions of Ambroise Paré don't match one authentic portrait.
- The iconography used for Apollonius of Perga was meant for another man.
- The missing portrait of Robert Hooke. Did Newton really destroy it?
- Lisa Jardine's enduring blunder hinders the depictions of two scientists.
- Tribulations of a great portrait of Jan Baptist Van Helmont (1577-1644).
- Dubious quotations: Who really said that?
- Exact sexagesimal ratios in Pythagorean triples. Set in clay (c. 1800 BC).
- Extant mathematical papyri betray the Egyptian taste for recreational mathematics.
- Classical geometry describes an homogeneous space indifferent to scale.
- Anthyphairesis is more elementary than factorization into primes.
- Obliquity of the ecliptic in the time of Eratosthenes (276-194 BC).
- Vertical wells at Syene are completely sunlit only once a year, aren't they?
- Eratosthenes sizes up the Earth: 700 stadia per degree of latitude.
- Knowing the Earth is round. Astronomical and terrestrial obsrvations.
- The distance to the Moon was computed by Aristarchus and Hipparchus.
- Latitude and longitude: The spherical grid of meridians and parallels.
- Itinerary units: The land league and the nautical league.
- Amber, compass and lightning: Glimpses of electricity and magnetism.
- The Antikythera Mechanism (c. 87 BC) is the oldest known orrery.
- Music theory: Design of musical instruments and study of harmony.
- The cult of Pythagoras.
- On the nature of physical laws: The example of gravitation.
- Controlled Experiment: A concept attributed to Sir Francis Bacon (1590).
- History of the Scientific Method.
- Distinguishing between Science and Pseudoscience.
- Faster-than-light neutrinos? How the media butchers the scientific method.
- What is time? Why don't we remember the future?
- The beginning of time. Was there anything before that?
- Time machines: Unavoidable microscopically, impossible macroscopically.
- Determinism precludes the arrow of time.
- GPS time is now universally available, fairly inexpensively.
- Cosmic time is the time kept by a free-falling clock at rest in its local CMB.
- Introduction: Geometry, statics, kinematics, dynamics and beyond...
- The notion of force. Statics, mechanical advantage and virtual work.
- Speed. Allowing the division of unlike quantities (distance and time).
- Mean-speed theorem. The distance traveled at constant acceleration.
- The timing experiments of Galileo: From the pendulum to falling bodies.
- The true period of a pendulum is proportional to 1 / agm ( 1 , cos A/2 ).
- The parabola of a cannonball, compared to Aristotle's triangular path.
- Conservation of momentum is key to Newton's three laws of motion.
- The work done to a point-mass equals the change in its kinetic energy.
- Relativistic work done and the corresponding change in relativistic energy.
- Relativistic thermodynamics: A point-mass endowed with internal heat.
- Spacecraft speeds up upon reentry into the upper atmosphere.
- Lewis Carroll's monkey climbs a rope over a pulley, with a counterweight.
- Two-ball drop can make one ball bounce up to 9 times the dropping height.
- Normal acceleration = Square of speed divided by the radius of curvature.
- Roller-coasters must rise more than half a radius above any loop-the-loop.
- Conical pendulum: A hanging bob whose trajectory is an horizontal circle.
- Conical pendulum constrained by a hemisphere: The string tension.
- Ball in a Bowl: Pure rolling increases the period of oscillation by 18.3%.
- Hooke's Law: Simple harmonic motion of a mass suspended to a spring.
- Speed of an electron estimated with the Bohr model of the atom.
- Hardest Stuff: Diamond is no longer the hardest known material.
- Hardness is an elusive nonelastic property, distinct from stiffness.
- Hot summers, hot equator! The distance to the Sun is not the explanation.
- Kelvin's Thunderstorm: Using falling water drops to generate high voltages.
- The Coriolis effect: A dropped object falls to the east of the plumb line.
- Terminal velocity of an object falling in the air.
- Angular momentum and torque. Spin and orbital angular momentum.
- Ad hoc conserved quantities unrelated to energy or momenta.
- Rotation vector of a moving rigid body (and/or "frame of reference").
- Angular momentum equals moment of inertia times angular velocity.
- Kinetic energy of a solid: Sum of its translational and rotational energies.
- Moments about a point or a plane are convenient mathematical fictions.
- Perpendicular Axis Theorem: Axis of rotation perpendicular to a lamina.
- The Parallel Axis Theorem: Moment of inertia about an off-center axis.
- Moment of inertia of a thick plate, derived from the parallel axis theorem.
- Moment of inertia of a right cone or conical frustum.
- Momenta of homogeneous bodies. List of common examples.
- Rigid pendulum moving under its own weight about a fixed horizontal axis.
- Reversible pendulum. The same period around two distinct axes.
- Moment of inertia of a spherical distribution or an homogeneous ellipsoid.
- Moment of inertia of the Earth is equal to 0.330695 M a 2.
- Second dynamic form factor (J2) of a mass distribution.
- Axial precession: Reaction of a gyroscope to a torque across its axis.
- Elbow in free space: Muscle acting on two solids around a common axis.

- All physical theories have a limited range of validity.
- Gravity vs. Electrostatics: Straight comparisons.
- Binet's formulas: Deriving Kepler's laws for two orbiting bodies.
- The celerity hodograph of a body in elliptical orbit is a perfect circle !
- Airy weighs the Earth by timing a pendulum deep in a mine.
- Rigid equilateral triangle formed by three gravitating bodies.
- The five Lagrange points of two gravitating bodies in circular orbit.
- Geosynchronous Orbit: Semimajor radius of 36000 km around the Earth.
- Hohmann transfer orbit: From one circular orbit to another in two kicks.
- The gravitational self-energy of a ball (mass M, radius R) is -1.2 GM2/R
- Orbital Mechanics. Description of orbital motion using orbital elements.
- Tides on Earth: Dominant rôle of the Moon. Lesser rôle of the Sun.
- Attraction between rigid bodies, not necessarily spherically symmetric.
- Asteroid 99942 Apophis: Near-Earth objects and gravitational keyholes.
- Mass distributions of galaxies. Evidence for the existence of dark matter.
- Coefficients of friction: The static coefficent exceeds the kinetic one.
- Example involving a nontrivial choice between static and kinetic regimes.
- Minimum inclination of a ladder leaning against a frictionless wall.
- Spinning cylinder on an horizontal plane: The skidding before pure roll.
- Walter Lewin's Effect: Drawing a dotted line on a blackboard.
- Coefficient of restitution (e) Ratio of initial to final closing speed.
- Leonardo da Vinci's Friction Arch : Straight planks, no nails...
- Billiards and pool tables: Nominal & quoted size, play area and clearance.
- Slate slab: The playing surface is cloth-covered rock.
- Billiard balls: Phenolic resin binding a dense powder has replaced ivory.
- Cue sticks: Butts and shafts. Basic construction. Anti-squirt technology.
- The contents of a cue case reflect the player's basic choices.
- Cue tips. Leather and phenolic tips.
- Two types of billiard chalk to reduce hand friction or increase tip friction.
- Silicon spray can be used by trickshot artists to reduce ball-cloth friction.
- Normal trajectory of a billiard ball: A parabola followed by a straight line.
- Making the cue ball stop after hitting the object ball.
- The stun path ("tangent line").
- The impossible 90° cut-shot made possible with extreme english.
- Squirt between cue and cue ball with extreme English (vertical spin axis).
- Jump shots. Legal and illegal ways to send the cue ball up in the air.
- Concave mirrors create enlarged virtual images of objects in front of them.
- Thin-lens equation. How the positions of an object and its image are tied.
- Focusing distance: The distance between an object and its image.
- Hyperfocal distance. Nearest in-focus objects when lens is set to infinity.
- Matrix methods: Transformations of a ray's inclination and radial distance.
- A crystal ball (index n and radius R) has focal length f = R / (2n-2).
- Lens-maker's formula: Focal lens as a function of signed curvatures.
- Thin-lenses are rectilinear: The image of a straight line is straight.
- Galileo's refractor (1609). Based on a design by Hans Lippershey (1608).
- Reflecting telescopes: The simplest design is due to Isaac Newton (1668).
- The compound microscope: Combining an object lens and an eyepiece.
- Distortion: When the image of a straight line ain't straight.
- The image of a tilted plane is a plane, which it intersects on the lens plane.
- Gullstrand's formula: Power of two lenses separated by a distance.
- Light falls off as cos4 q
(where q = angular distance to the image center).
- Retrofocus allows a wide-angle image to be produced by a remote lens.
- Numerical aperture doesn't depend on the refraction index.
- Angular resolution varies as the wavelength and inversely as the diameter.
- Opposition effect increases albedo by eliminating micro-shadows.
- Honeycomb grids attenuate drastically the peripheral parts of a light beam.
- Schlieren imaging shows how shockwaves disturb the refractive index (n).
- A brief history of light: From Empedocles to modern times.
- Luminous units of measurement: Light as the human eye sees it.
- Monochromacy. In dim light, humans see in black-and-white.
- Dichromacy. 8% of men and 0.64% of women are color-blind.
- Trichromacy. Normal photopic vison (bright-light). 3 primary colors.
- Tetrachromacy. Mysteries of the fourth primary color.
- Aphakia. The eye of Claude Monet was sensitive to UV light.
- Light polarization is easy to demonstrate with sheet polarizers (sunglasses).
- Technical jargon: Different manufacturers promote different terms.
- Pinhole camera: The simplest camera doesn't even have a lens.
- Simple lens. Focal length. Aperture. f-stops.
- Microphotography. Using a lens backward in front of another.
- Depth of field. Circle of confusion. Hyperfocal distance.
- Bokeh: The aspect of out-of-focus areas.
- Defocus control (DC). Enhancing the bokeh of either near or far regions.
- Smooth transition focus. Optical apodization provides perfect bokeh.
- Lens sharpness. Center resolution, corner resolution. Vignetting.
- Stabilizers: Image stabilization (IS) = vibration reduction (VR).
- Color-corrected lenses. Color dispersion of various types of glass.
- Zoom lens. Adjustable focal length (can be internal or not).
- Focusing. Manual focusing. Focus detection.
- Professional cameras. Evolution toward ruggedness and full sensor size.
- Autofocus: Focusing motors attached to the lens or the camera.
- Focus breathing. Effective focal length may depend on focusing distance.
- Macro darkening. Effective aperture is lower in close-up photography.
- ISO sensitivity is directly derived from the old ASA & DIN standards.
- Light-sensitive films: Chemistry, sensitivity and grain size.
- Electronic photocells. Capturing an image one pixel at a time.
- Signal to noise ratio is limited by the number of photons per pixel.
- Bayer filters give color-vision to large arrays of photodiodes.
- Digital image sensors. Sizes, spatial resolution and color depth.
- Crop factor: 43.2666153 mm divided by the diagonal of the sensor.
- Handheld shots: Shutter speed should exceed equivalent focal length.
- Spatial filters. Lowpass filters or lack thereof. ADC resolution loss.
- Formats. Digital encoding of still pictures: raw, jpeg, etc.
- Exposure. Exposure index (and corrections for long exposure).
- Mounts: The various ways of attaching a body to interchangeable lenses.
- Screw-on filters have a 0.75 mm pitch and a few standard diameters.
- Neutral density filters. Changing exposure at constant speed and aperture.
- Photographing the Sun. ISO 100, 1/4000 s, f/32, with an ND1000 filter.
- Cut filters: Blocking parts of the IR, visible and/or UV spectra.
- Color temperature. Light sources and white balance.
- Shadows on a sunny day. How dark and how blue are they really?
- Color conversion: Converting one color temperature to another.
- Flash photography. Technology. Guide number (GN) & duration control.
- Huygens' Principle. A convenient fiction to describe wave propagation.
- Diffraction occurs when when a wave emanates from a bounded source.
- Young's double-slit experiment demonstrates the wavelike nature of light.
- Celerity is the speed with which phase propagates.
- Standing waves feature stationary nodes and antinodes.
- Snell's Law gives the angle of refraction (Thomas Harriot, July 1601).
- Total internal reflection (TIR) at incidences exceeding the critical angle.
- Birefringence. Discovery of polarization (Erasmus Bartholinus, 1669).
- Fresnel equations: Reflected or refracted intensities of polarized light.
- Brewster's angle is the incidence which yields a 100% polarized reflection.
- Stokes parameters: A standard description of the state of polarization.
- Transverse wave on a rope: (celerity) 2 = (tension) / (linear mass density).
- Chladni patterns: The lines formed by nodes in an oscillating plate.
- Wave inertia: The idea behind the Hemispherical Resonator Gyroscope.
- Dispersion relation: Pulsatance vs. wave number; frequency vs. wavelength.
- Empirical approximations often give wavelength as a function of frequency.
- Group velocity is the traveling speed of a beat phenomenon.
- Rayleigh scattering makes the sky blue and sunsets red.
- Index of refraction of water for light of different colors.
- A spherical drop reflects light back (red up to 42.34° & violet up to 40.58°).
- The length of a rainbow: Mathematical digression.
- Wavelength: 940 nm (319 THz) is the most common specification for IR.
- Modulation: 38 kHz (38.4 kHz). Also: 30, 33, 36, 36.7, 40, 56, 455 kHz.
- Remote shutter release for cameras. The simplest type of infrared control.
- On/off patterns to encode data bits and the start/stop of data frames.
- Unexplained datasheet mysteries. Why are Rohm's specs slightly off?
- Discrete IR control codes provide critical functions for automated control.
- RECS-80: An obsolete system, proposed by Philips in 1988.
- RC-5 and RC-6. Philips and the well-documented European protocol.
- NEC Protocol. The Japanese format.
- SIRC Protocol by Sony.
- RCA Protocol: 64 ms to send a 4-bit address and 8-bit data at 56 kHz.
- HP 82240B: The standard printer for HP scientific calculators, since 1989.
- Philips Pronto universal remotes. Pronto codes for learned commands.
- Databases of IR codes: Defending consumers & creating flexibility.
- Serial protocol: 2400 Bd, 1 start bit, 8 data bits, 1 stop bit, odd parity.
- Resurrrecting 455 kHz modulation to transmit at high-speed (19200 Bd).
Lasers : From masers to laser beams
- Stimulated emission is crucial to blackbody equilibrium (Einstein, 1916).
- Bose-Einstein Statistics is what explains stimulated emission of bosons.
- Optical pumping is the key to creating a population inversion.
- Population inversion : When energetic states are abnormally abundant.
- LASER Cavity. Light Amplification by Stimulated Emission of Radiation.
- Gaussian beam. The shape of an ideal laser beam.
- Tunable lasers.
- Negative tenperature of a laser.
- Fermat's principle (least time) for light (c.1655) predates Newton.
- Maupertuis principle of least action (1744).
- Virtual Work: A substitute for Newton's laws that cancels constraint forces.
- Phase Space: Phase describes completely the state of a classical system.
- Either velocities or momenta are added to configuration to specify a phase.
- The Lagrangian is a function of positions and velocities.
- The Hamiltonian depends on positions and momenta.
- Poisson brackets: An abstract synthetic view of analytical mechanics.
- Liouville's theorem: The Hamiltonian phase volume doesn't change.
- Noether's theorem: Conservation laws express the symmetries of physics.
- Relativistic point-mass: Lagrangian, Hamiltonian and free momentum.
- Charge in a magnetic field: The canonical momentum isn't the linear one.
- Fokker lagrangian: Lagrangien formulation of general relativity (1924).
- Field theory: Lagrangian function of a continuum of values and velocities.
- Clarifications: Vector calculus (Heaviside) & microscopic view (Lorentz).
- The vexing problem of units is a thing of the past if you stick to SI units.
- The Lorentz force on a test particle defines the local electromagnetic fields.
- Electrostatics (1785): The study of the electric field due to static charges.
- Electric capacity is an electrostatic concept (adequate at low frequencies).
- Electrostatic multipoles: The multipole expansion of an electrostatic field.
- Birth of electromagnetism (1820): Electric currents create magnetic fields.
- Biot-Savart Law: The static magnetic induction due to steady currents.
- Magnetic scalar potential: A multivalued static scalar field.
- Magnetic monopoles do not exist : A law stating a fact not yet disproved.
- Ampère's law (1825): The law of static electromagnetism.
- Faraday's law (1831): Electric circulation induced by magnetic flux change.
- Self-induction received by a circuit from the magnetic field it produces.
- Ampère-Maxwell law: Dynamic generalization (1861) of Ampère's law.
- Putting it all together: Historical paths to Maxwell's electromagnetism.
- Maxwell's equations unify electricity and magnetism dynamically (1864).
- Continuity equation: Maxwell's equations imply conservation of charge.
- Waves: Predicted by Faraday, Maxwell & FitzGerald. Observed by Hertz.
- Electromagnetic energy density and the flux of the Poynting vector.
- Planar electromagnetic waves: The simplest type of electromagnetic waves.
- Maxwell-Bartoli radiation pressure. First detected by P. Lebedev in 1899.
- Electromagnetic potentials are postulated to obey the Lorenz gauge.
- Solutions to Maxwell's equations, as retarded or advanced potentials.
- Electrodynamic fields corresponding to retarded potentials.
- Electrodynamic fields corresponding to advanced potentials.
- The gauge of retarded potentials: is it really the Lorenz gauge?
- Power radiated by an accelerated charge: The Larmor formula (1897).
- Lorentz-Dirac equation for the motion of a point charge is of third order.
- Capacitance is measured in farads (F).
- Capacity of a sphere. Single-electrode capacitor.
- Parallel-plates: Two large planar electrodes separated by a small surface d.
- Cylindrical wires or shielding. Many possible configurations.
- Leyden jars. Earliests high-voltage capacitors.
- Ultracapacitors: One farad or more.
- Molecular electric dipole moments. First studied by Peter Debye in 1912.
- Force exerted on a dipole by a nonuniform field.
- Torque on a dipole is proportional to its cross-product into the field.
- Electric and magnetic dipoles: Dipolar solutions of Maxwell's equations.
- Static distributions of magnetic dipoles can be emulated by steady currents.
- Static distributions of electric dipoles are equivalent to charge distributions.
- Field at center of a uniformly magnetized or polarized sphere of any size.
- Sign reversal in magnetic and electric fields from matching dipoles.
- Relativistic dipoles: A moving magnet develops an electric moment.
Magnetism; Electromagnetic Properties of Matter
- Magnetization and polarization describe densities of bound dipoles.
- Distinct magnetization and polarization gauges may yield the same field.
- Maxwell's equations in matter: Electric displacement & magnetic strength.
- Electric susceptibility is the propensity to be polarized by an electric field.
- Electric permittivity and magnetic permeability. Related to susceptibilities.
- Paramagnetism: Weak positive susceptibility.
- Diamagnetism: Lorentz force turns orbital moments against an external B.
- Magnetic levitation: How to skirt the theorem of Samuel Earnshaw (1842).
- Pyrolytic carbon: The most diamagnetic substance, at room temperature.
- Bohr-van Leeuwen Theorem: Diamagnetism and paramagnetism cancel ?!
- Thermodynamics of dielectric matter: dU = E.dD + ...
- Ferromagnetism: Permanent magnetization without an external field.
- Antiferromagnetism: When adjacent dipoles tend to oppose each other...
- Ferrimagnetism: With two kinds of dipoles, partial cancellation may occur.
- Magneto-optical effect discovered by Faraday on September 13, 1845.
- Ohm's Law: Current density is proportional to electric field: j = s E.
- Bloch equations: Longitudinal and transverse magnetization relaxation.
- Cotton effect: Interaction of light with chiral molecules.
- The relativistic origin of magnetism.
- Magnetometry. How do you measure a permanent magnet?
- Make a magnet without using electric current or another magnet.
- Halbach arrays: Field is reinforced on one side and vanishes on the other.
- Homopolar motor: The first electric motor, by Michael Faraday (1831).
- Faraday's disk can generate huge currents at a low voltage.
- Magic wheels: Two repelling ring magnets mounted on the same axle.
- Beakman's motor. Current switches on and off as the coil spins.
- Tesla turbine. Stack of spinning disks with outer intake and inner outflow.
- Tesla coil. A low-current high-voltage generator.
- Schumann's cavity is resonating at 8 Hz, below the ionosphere.
- Mechanical switches. Working out proper snubber networks.
- Mechanical relays. Flyback diodes in parallel with DC-controlled coils.
- Diodes: PN, PIN, Silicium, Germanium, Schottky, Zener, varicap, etc.
- Temperature coefficients (tempco) and temperature compensation (TC).
- Operational amplifiers A quick survey of those indispensable analog ICs.
- Bipolar Junction Transistors (BJT) : NPN and PNP polarity types.
- Thyristor. GE's silicon-controlled rectifier (SCR) has 4 silicon layers.
- Triacs conduct in either direction once triggered, until current drops to zero.
- A diac is turned on by a large voltage. It turns off when current is too low.
- Field-programmable gate arrays (FPGA). Digital flexibility at high speed.
- Hall effect. The classical effect discovered by Edwin Hall in 1879.
- Aristotle's plenism. Downfall of the Horror Vacui doctrine (17th century).
- Sprengel's pump (1865) made Crookes tubes and lightbulbs possible.
- Vacuum tubes. Heated filaments, grids and electrons moving in a vacuum.
- Dirac's equation predicted positrons as holes in a bizarre vacuum.
- The Quantum Vacuum. The vacuum isn't empty. Structure of the vacuum.
- Observers in motion: An elementary derivation of the Lorentz Transform.
- Combining parallel velocities never results in a speed exceeding c.
- Combining velocities when they're not collinear.
- The headlight effect: An isotropic source will radiate forward if it moves.
- Closing speed: The distance between objects may change faster than c.
- Fizeau's empirical relation between refractive index (n) and Fresnel drag.
- Harress-Sagnac effect. Measuring angular motion with fiber optic cable.
- The rapidity concept simplifies the relativistic addition of speeds.
- Relative velocity of two photons: Undefined if they have the same direction
- Minkowski spacetime. Lorentz transform applies to 4-vector coordinates.
- The Lorentz transform expressed vectorially for a boost of speed V.
- Wave vector: The 4-dimensional gradient of the phase describes a wave.
- Doppler shift: The relativistic effect is not purely radial.
- Relativistic momentum and Einstein's relation between mass and energy.
- Kinetic energy: At low speed, the relativistic energy varies like
½ mv 2.
- Photons and other massless particles: Finite energy at speed c.
- The de Broglie celerity (u) is inversely proportional to a particle's speed.
- Compton diffusion: The result of collisions between photons and electrons.
- The Klein-Nishina formula: gives the cross-section in Compton scattering.
- Compton effect is suppressed for visible light and bound electrons.
- Elastic shock: Energy transfer is v.dp. (None is seen from the barycenter.)
- Photon-photon scattering is like an elastic collision of two photons.
- Cherenkov effect: When an electron exceeds the celerity of light...
- Constant acceleration over an entire lifetime will take you pretty far.
- Langevin's twins paradox. Confirmed by the Häfele-Keating experiment.
- Terrell effect. Apparent rotation of a fast-moving body.
- Photons are quanta of light. They're both wavelike and corpuscular.
- The photoelectric effect was explained by Albert Einstein in 1905.
- Signal-to-noise ratio of light sensors: The ultimate physical limit.
- Soft photons carry (almost) no energy but still have unit spin.
- Henri Becquerel and the [second] discovery of natural radioactivity (1896).
- Pierre & Marie Curie: The discovery of new radioactive elements (1898).
- Rutherford lead-block experiment. The three types of ionizing radiations.
- Radioactive-decay law was formulated by Rutherford and Soddy, in 1902.
- Geiger-Marsden experiment: There's a tiny dense nucleus inside the atom!
- Alpha-decay: Polonium (Po-210, Z=84) decays into Lead (Pb-206, Z=82).
- Mass Defect: In a nuclear reaction, the Q-value balances the mass change.
- The standard decay modes:
a, b-, 2b-, b+, e (electron capture) or IT.
- The 4 radioactive series: Thorium, Neptunium, Uranium and Actinium.
- Other decay modes: Proton or neutron emission, fission and spallation.
- The Geiger counter measures the activity flux of ionizing radiation.
- Scintillation allows quantitive measurements of a gamma spectrum.
- Cross-section: A target looks as if its size depends on the projectile's speed.
- Artificial radioactivity: Neutron bombardment creates unstable nuclides.
- Chain reactions: When neutron-induced decays produce more neutrons...
- Critical mass: The smallest mass that will allow runaway chain reactions.
- Thermonuclear bombs. Nuclear fusion ignited by fission devices.
- Carbon-dating: Radiocarbon ratio starts decaying when an organism dies.
- Fusion of deuterons: Helium is formed with liberation of energy.
- The Proton-Proton chain fusion powers all stars less than 1.5 solar masses.
- Catalytic nuclear reactions. The CNO cycle yields 7% of the Sun's power.
- Triple-Alpha process explains the abundance of Carbon and Oxygen,
- Tokamak reactors: Deuterium-Tritium fusion (DT) is the easiest to ignite.
- Farnsworth-Hirsch fusor: Controlled fusion on a desktop. Neutron source.
- Polywell reactor: The design advocated by the late Robert Bussard.
- Amateur nuclear physics: Demystifying nuclear energy and radioactivity.
- The Radioactive Boyscout and other misguided experimenters.
- Natural fission reactors. Predicted in 1956. Discovered in Gabon in 1972.
- Safe reactors: Fast automatic shutdown using UZrH fuel rods.
- Muon-facilitated nuclear fusion occurs at low temperatures (Frank, 1947).
- Cathode-ray tubes (CRT, 1875). Due to William Crookes (1832-1919).
- X-rays were discovered in 1895 by Wilhelm Röntgen (1845-1923).
- Bragg peak (1903). An ionizing ray loses a lot of energy near its demise.
- X-rays crystallography (XRC) was founded by Max von Laue, in 1912.
- Synchrotron radiation is produced by bending a beam of charged particles.
- Brehmsstrahlung: The radiation emitted by decelerating charged particles.
- Dose deposited by radiation in human tissue. 1 Sv = 1 J/kg = 100 Rem.
- Pauli deduced the existence of the neutrino from conservation laws.
- Fermi theory of beta decay (1934).
- Direct detection of neutrinos. Cowan-Reines neutrino experiment (1956).
- Parity violation was established by the Wu experiment (1956).
- Discovery of the muon-neutrino. Steinberger, Lederman, Schwartz (1962).
- Neutrino oscillations. Solar neutrinos revealed nonzero neutrino masses.
- Confined color charges. Only color-neutral particles can be observed.
- Isospin (isotopic spin) is like spin in a disembodied Hilbert space.
- Bootstrap principle by Geoffrey Chew and Steve Frautschi (1961).
- The 8 Gell-Mann matrices. SU(3) is an eight-dimensional Lie group.
- Quantum Chromodynamics (QCD). The way color charges are traded.
- Deep inelastic scattering of electrons by protons or bound neutrons (1967).
- Renormalization of Yang-Mills (gauge) theories ('t Hooft, 1971).
- Asymptotic freedom of the strong force at small distances (1973).
- Scintillation counter. Invented by William Crookes in 1903 (using ZnS).
- Geiger counter. Counting ionizing particles by the avalanches they cause.
- Cloud chamber. Mist condenses first along the tracks of ionizing particles.
- Nuclear emulsions: Latent images are produced along particle tracks.
- Bubble chamber. Nucleation occurs along trails left by ionizing particles.
- Wire chamber (1968). Multi-wire proportional chamber (MWPC).
- Electrostatic generators. Accelerating charged particle with electric fields.
- Linear accelerators (1924). Using waves rather than static electric fields.
- Cyclotron (1929). A constant magnetic field creates spiraling trajectories.
- Betatron (1934). Accelerating electrons with a changing magnetic field.
- Microtron (1944). Modified cyclotron needing only small electrodes.
- Synchrotrons (1944, 1945). Modern circular particle accelerators.
- Strong focusing of charged beams, using alternating gradients.
- Large Hadron Collider (LHC). The largest circular accelerator ever.
- Wakefield accelerators. Particles surfing the wake of a laser in a plasma.
Supersymmetry between bosons and fermions
- History of Supersymmetry (SUSY).
- The Wess-Zumino-Witten model (WZW).
- Unification: Consistency is required. Actual high-energy unification is not.
- Kaluza-Klein Theory: Postulating an extra dimension for electromagnetism.
- 1960's hadron physics: Regge trajectories begat constant-tension strings.
- Gabriele Veneziano: The magic of Euler's beta and gamma functions.
- Leonard Susskind (1940-): The basic idea of a fundamental string.
- Joël Scherk (1946-1979) & John Schwarz: Rediscovering gravity.
- Michael Green & John Schwarz: Hoping for a Theory of Everything.
- String Quintet: Five different consistent string theories!
- M-Theory: Ed Witten's 11-dimensional brainchild, unveiled at String '95.
- The brane world scenarios of Lisa Randall and Burt Ovrut.
Quantum Gravity: Toward a theory of everything (TOE).
- Wheeler-DeWitt equation (WdW). The basis for loop quantum gravity.
- Loop Quantum Gravity (LQG).
- Anti-de Sitter space (AdS).
- Conformal field theory (CFT).
- Maldacena duality: AdS/CFT correspondence (1997).
- AMPS Firewall: Almheiri, Marolf, Polchinski, and Sully (2012).
- Fluid mechanics: Tracking actual particles.
- Atmospheric pressure varies vertically in proportion to the density of air.
- The Magdeburg hemispheres are held together by more than a ton of force.
- The ideal gas laws of Boyle, Mariotte, Charles, Gay-Lussac, and Avogadro.
- Joule's law: Internal energy of an ideal gas depends only on temperature.
- Deflating a tire: Releasing a pressurized gas into the atmosphere.
- The Van der Waals equation and other interesting equations of state.
- Virial equation of state. Virial expansion coefficients. Boyle's temperature.
- Viscosity is the ratio of a shear stress to the shear strain rate it induces.
- Permeability and permeance: Vapor barriers and porous materials.
- Resonant frequencies of air in a box.
- The Earth's atmosphere. Pressure at sea-level and total mass above.
- Composition of dry air at sea level (for 450 ppm carbon dioxide).
- Humidity. The moisture content of clear atmospheric air.
- The first hot-air balloon (Montgolfière) was demonstrated on June 4, 1783.
- Sulfur hexafluoride is a very heavy gas and a good electrical insulator.
- Virial of force: A dynamic quantity defined by Rudolf Clausius in 1870.
- Virial. The classical virial of momentum is a conserved quantity.
- The relativistic virial is defined at constant time in the observer's frame.
- Quantum virial: The quantum counterpart of the classical virial.
- Viscosity: The transport of microscopic momentum.
- Brownian motion and Einstein's estimate of molecular sizes.
- Thermal Conductivity: The transport of microscopic energy.
- Diffusivity: The transport of chemical concentration.
- Boltzmann Transport Equation: Solve for a continuous random variable.
- Speed of Sound: Reversible transport of a pressure disturbance in a fluid.
- The speed of sound in the atmosphere varies with altitude.
- Newton's formula is off by 15.48% under (bad) isothermal assumptions.
- Speed of sound in a fluid, computed under (good) isentropic assumptions.
- Perceived loudness differs from absolute (physical) loudness of sound.
- Acoustical limits: Sound waves have a limited frequency range.
- Western origins. Gregorian modes just denoted specific vocal octaves.
- Note durations follow a binary progression. Dotting prolongs by 50%.
- Tempo: The speed of music. What the metronome measures.
- Beats of the metronome. Bar (measures) and time signatures.
- Triplet: Group of 3 notes equally splitting twice their common duration.
- Dynamics. Pianissimo to fortissimo. Diminuendo or crescendo.
- The Frequency Domain: Sound reduces to a superposition of tones.
- Perfect pitch: Native music speakers can easily name any absolute pitch.
- Legacy pitch and marketing hype.
- Staves and clefs. Transcribing and reading musical notes.
- Common keyboards. From double-octave (25 keys) to full piano (88 keys).
- Musical intervals are ratios of frequencies.
- Quantifying the beauty of consonances: Euler's gradus function (1730).
- The circle of fifths: Best fit for the two simplest harmonies (2:1 and 3:2).
- Tritone: Half an octave. A dissonant interval (F to B or B to F).
- Scales. The key of C major (or A minor) only uses white piano keys.
- The 7 modes of the major scale (diatonic modes) including natural minor.
- Brightness and darkness. Canonical quantification of an elusive concept.
- Non-diatonic minor scales: Melodic minor and harmonic minor.
- Harmonic major scale. The mirror inverse of the harmonic minor scale.
- Other noteworthy heptatonic scales and Bebop scales (with passing tones).
- Hexatonic scales: Whole-tone. Augmented. Prometheus. Blues scale.
- Two diminished scales: Whole-half diminished & half-whole diminished.
- Chords are separate notes played together.
- Harmonization.
- Cadence: Resolution of tension. Musical punctuation and closure.
- Modulation and key changes.
- Composing 101: Some basic principles composers have been perusing.
- Musical Dice: Composing music without human intervention (1757).
- Ornaments and embellishments: Superficial changes respecting the melody.
- Octave displacement (Octave dispersion).
- Jazz: Lydian Chromatic Concept of Tonal Organization (George Russell).
- MIDI: Musical Instrument Digital Interface (1980).
- Microtonal instruments and exploration of polychromatic music.
- Guitars and other fretted musical instruments.
- Classical fretless 4-string instruments. The violin family.
- Recorders. Wooden flipple flutes produce pure tones with little harmonics.
- 4 heptatonic scales have signatures without double alterations in all 12 keys.
- The 7 diatonic modes include the major mode and natural minor.
- Brightness and darkness. Canonical quantification of an elusive concept.
- Non-diatonic minor scales: Melodic minor and harmonic minor.
- Harmonic major scale. The mirror inverse of the harmonic minor scale.
- Double-harmonic major scale. Each of its 7 modes has one cursed key.
- Hungarian major scale and Romanian major scale are non-cohemitonic.
- Neapolitan Major is palindromic. Neapolitan minor is Major b2 inverted.
- The Blues leading-tone scale is the inverse of the Persian scale.
- The Major flat-5 scale and its interesting modes.
- Half a dozen Bebop modes in three distinct scales.
- Enigmatic scales: Minor, ascending, descending and (octonic) mixed.
- The Egyptian Crater scale of Jeff Buset (2009).
- Petra's Crater scale. (2019). The most imperfect heptatonic scale.
- Complex pulsatance: s =
s+iw (damping constant + imaginary pulsatance)
- Complex impedance: Resistance and reactance.
- Quality Factor (Q). Ratio of maximal stored energy to dissipated power.
- Nullators and norators: Strange dipoles for analog electronic design.
- Corner frequency of a simple first-order low-pass filter. -3 dB bandwidth.
- Second-order passive low-pass filter, with inductor and capacitor.
- Two cascaded RC low-pass filters can almost achieve critical damping.
- Sallen-Key filters: Active filters do not require inductors.
- Lowpass Butterworth filter of order n : The flattest low-frequency response.
- Linkwitz-Riley crossover filters used in modern active audio crossovers.
- Chebyshev filters: Ripples in either the passband or the stopband.
- Elliptic (Cauer) filters encompass all Butterworth and Chebyshev types.
- Legendre filters maximal roll-off rate for monotonous frequency response.
- Gegenbauer filters: From Butterworth to Chebyshev, via Legendre.
- Phase response of a filter.
- Bessel-Thomson filters: Phase linearity and group delay.
- Gaussian filters: Focusing on time-domain communication pulses.
- Linear phase equiripple: Ripples in group delay to go beyond Bessel filters.
- DSL filters allow POTS below 3400 Hz & block digital data above 25 kHz.
- Switched capacitor: Faking a resistor with a capacitor and a SPDT switch.
- Raising the Titanic, with (a lot of) hydrogen.
- Gravitational Subway: From here to anywhere on Earth, in 42 minutes.
- In a vacuum tube, a drop to the center of the Earth would take 21 minutes.
- Detecting a single graviton is an impossible task.
- Controled fusion: Why the Tokamak approach can't produce energy.
- Solid wood: Some common lumber and exotic woods.
- Lumber (timber). Primary stock obtained from logs.
- Composite boards. From paperboard and cardboard to phenolic hardboard.
- Carpenter's glues. Physics & chemistry of wood glues. Cyanoacrylate glue.
- Clamps. Gluing any wood joint requires adequate clamping.
- Axe and adze: Two related tools which date back to the Stone Age.
- Drawknife, travisher and spokeshave. Ancient tools predating planes.
- Hand planes: The art of removing high-spots, using a sole as reference.
- Power planers: Flatness and uniform thickness from jointers and planers.
- Joinery: The various types of joints to choose from.
- Portable bench, vise & dogs. In praise of the Workmate 425 and others.
- Mallets and hammers.
- Metal fasteners: Nails, wood screws and Twinfast screws. Nuts & bolts.
- Dowels and treenails Locking reinforced joints in all-wood construction.
- Chisels.
- Whittling and carving.
- Hand saws and their uses.
- Table saw. Rip fence and pushblock. Miter gauge or cross-cut sleds.
- Other saws with circular blades: Trim saw, miter saw, radial-arm saw.
- Power-saws with non-circular blades: Bandsaw, jigsaw, reciprocating saw.
- Drills and drill bits. Hand drill. Handheld power drill. Drill press.
- Turning wood on a lathe.
- Awls and trammel points. Beam compass.
- Calipers and dividers.
- Files and rasps.
- Sanding.
- Dust collection. Cyclone or Thien baffle before vacuum dust extractor.
- Staining and distressing. Accenting wood grain and tooling marks.
- Sealing and priming. Sealing wood pores.
- Finishing: Applying tint, paint, lacquer, varnish...
- Extracting metals: Ores. Mining. Smelting. Recycling.
- Alloys. Physics and chemistry of alloys. Engineering grades.
- Sheet metal. Most metals or single-phase alloys can be rolled into sheets.
- Welding, soldering and brazing. Joining metal pieces without fasteners.
- Measuring. Calipers, micrometer, surface plate, surface gauge.
- Machinist vise. Holding metal pieces in place while working on them.
- Sawing and cutting. Adjustable hacksaw and jeweler's saw.
- Filing and grinding.
- Drills. Handheld drills and drill presses. Drill bits.
- Milling. Making straight or curved cuts.
- Lathe. Turning and machining.
- Engine turning.
- Taps. Threading holes or rods.
- Circular champfers. Mandatory external chamfer for off-the-shelf bolts.
- Gunsmithing. Some gun parts are illegal to make without a license.
- Finishing. Polishing, brushing.
- Chemical surface treatments. Blueing steel. Anodizing aluminum.
- Painting and coating.
- Forging hot iron pieces. A blackmith hammers them on an anvil.
- Electrical Discharge Machining (EDM). Electric arcs as cutting tools.
- The aeolipile. Ancient steam engine demonstrating jet propulsion.
- Edward Somerset of Worcester (1601-1667): Steam fountain blueprint.
- Denis Papin (1647-1714): Pressure cooking and the first piston engine.
- Thomas Savery (c.1650-1715): Two pistons and an independent boiler.
- Thomas Newcomen (1663-1729) & John Calley: Atmospheric engine.
- Nicolas-Joseph Cugnot (1725-1804): The first automobile (October 1769).
- James Watt (1736-1819): Steam condenser and Watt governor.
- Richard Trevithick (1771-1833) and the first railroad locomotives.
- Sadi Carnot (1796-1832): Carnot's cycle. The theoretical efficiency limit.
- Sir Charles Parsons (1854-1931): The modern steam turbine (1884).
- Drinking Bird: Room-temperature engine based on evaporative cooling.
- Elementary concept of temperature. The zeroth law of thermodynamics.


- Conservation of energy: The first law of thermodynamics.
- Increase of Entropy: The second law of thermodynamics.
- State variables: Extensive and intensive quantities.
- Entropy is missing information, a measure of disorder.
- Nernst Principle (third law): Entropy is zero at zero temperature.
- Thermodynamic potentials are convenient alternatives to internal energy.
- Calorimetric coefficients, adiabatic coefficient (g) heat capacities, etc.
- Relations between isothermal and isentropic coefficients.
- The thermal Grüneisen parameter.
- Entropy of a Van der Waals fluid as derived from its equation of state.
- Dulong-Petit Law (1819). The molar heat capacity of a metal is about 3 R.
- Thermal effects of molecular vibrations at moderate temperatures.
- Latent heat (L) is the heat transferred in a change of phase.
- Van 't Hoff's equation. How an equilibrium changes as temperature varies.
- Cryogenic coefficients: Lower temperature with an isenthalpic expansion.
- Peltier effect: Electrical cooling at a junction between dissimilar materials.
- Relativistic Thermodynamics: A moving body appears cooler.
- Inertia of energy for an object at nonzero temperature.
- Stefan's Law: A black body radiates as the fourth power of its temperature.
- The "Fourth Law": Is there really an upper bound to temperature?
- Hawking radiation: On the entropy and temperature of a black hole.
- Partition function: The cornerstone of the statistical approach.
- Elastic properties. Reversible deformations in resilient materials.
- Hysteresis and resilience. Stored elastic energy is never fully recovered.
- Elastomers. Unsaturated rubbers are cured by sulfur vulcanization.
- Coefficients ot thermal expansion: Cubical scalar and linear tensor.
- Invar anomaly: The low thermal expansion of 36% Ni / 86% Fe alloy.
- Waves in a solid: P-waves (fastest), S-waves, E-waves (thin rod), SAW...
- Thermodynamics of acoustics: Dynamic coefficients and isothermal ones.
- Rayleigh Wave: The quintessential surface acoustic wave (SAW).
- Laplace's Demon: Deducing past and future from a detailed snapshot.
- Maxwell's Demon: Happily trading information for entropy.
- Shockley's Ideal Diode Equation: Diodes don't violate the Second Law.
- Szilard's engine: Putting a simple-minded Maxwellian demon to work.
- Landauer's principle: The unavoidable thermodynamic cost of forgetting.
- Lagrange multipliers. One multiplier for each constraint of an optimization.
- Microcanonical equilibrium. Isolated system: All states are equiprobable.
- Equipartition of energy. Every degree of freedom gets an equal share.
- Canonical equilibrium: Boltzmann factor in a heat bath.
- Grand-canonical equilibrium when chemical exchanges are possible.
- Bose-Einstein statistics: One state may be occupied by many particles.
- Fermi-Dirac statistics: One state is occupied by at most one particle.
- Boltzmann statistics: The low-occupancy limit (most states unoccupied).
- Maxwell-Boltzmann distribution of molecular speeds in an ideal gas.
- Partition function: The cornerstone of the statistical approach.
- Fock basis for the tensor product of many identical Hilbert spaces.
- Quantum Logic: The surprising way quantum probabilities are obtained.
- Swapping particles either negates the quantum state or leaves it unchanged.
- The Measurement Dilemma: What makes Schrödinger's cat so special?
- Matrix Mechanics: Like measurements, matrices don't commute.
- Schrödinger's Equation: Nonrelativistic quantum particle in a classical field.
- Noether's Theorem: Conservation laws express the symmetries of physics.
Quantum Formalism :
- Kets are Hilbert vectors (duals of bras) on which observables operate.
- Hilbert space for a composite system. Tensor product of Hilbert spaces.
- Commutators give observables the structure of a Lie algebra.
- Some observables are associated with classical physical quantities.
- Uncertainty relations hold whenever the commutator does not vanish.
- Transverse certainties. Measuring two non-conjugate observables.
- Evolution with time of quantum states and average values.
- The time-energy uncertainty relation in nonrelativistic quantum theory.
- Spin is a form of angular momentum without a classical equivalent.
- Pauli matrices: Three 2 by 2 matrices with eigenvalues +1 and -1.
- Quantum Entanglement: The singlet and triplet states of two electrons.
- Bell's inequality is violated for the singlet state of two electron spins.
- KS theorem: Any definite values would violate physical relations (1967).
- Mach-Zehnder interferometer by Zehnder (1891) & Ludwig Mach (1892).
- Generalizations of Pauli matrices beyond spin ½.
- Density operators are quantum representations of imperfectly known states.
- Kubo-Martin-Schwinger (KMS) condition.
- Quantum stability of ordinary matter depends on electrons being fermions.
- Hamilton's analogy equates the principles of Fermat and Maupertuis.
- Box confinement by a finite potential in one dimension and 3 dimensions.
- Rotator: Quantization of the angular momentum.
- Harmonic oscillator.
- Coulomb potential: Classification of chemical orbitals.
- Wallis formula for p (1655). A quantum-mechanical derivation (2015).
- Any second-order linear equation reduces to Schrödinger's equation.
- Perturbative solution entails a divergent asymptotic series.
- Biographical facts about Serge Haroche: Genealogy, family and career.
- The Einstein box: A thought-experiment discussed by Einstein and Bohr.
- Micromaser: A closed cavity doesn't require perfect mirrors.
- Purcell effect: Enhancement of spontaneous fluorescence in a cavity.
- Quantum nondemolition measurements (QND) are almost classical.
- Circular Rydberg atom. The outer electron is in orbit at a large distance.
- Rydberg clock: Two superposed Rydberg states look like a rotating dipole.
- Jaynes-Cummings model (1963): 2-level atom in an optical cavity.
- Fabry-Pérot cavity.
- Superconductivity of Niobium.
- Fock basis. Quantum states where the number of photons is well-defined.
- The electromagnetic phase is the conjugate of the number of photons.
- Coherent states in electromagnetism (Roy J. Glauber, 1963).
- Light-shift effect (Claude Cohen-Tannoudji, 1961).
- Rabi escillations at 50 kHz (I.I. Rabi).
- Ramsey Interferometer (Norman Ramsey, 1949).
- Circuit QED. A solid-state counterpart of Cavity QED.
- Questions and Answers. Discussions related to the Haroche experiments.
- The Lamb shift. The original motivation for renormalization.
- Quantum Electrodynamics (QED) is the simplest quantum field theory.
- Second Quantization: Particles are modes of a quantized field.
- Elementary particles: Quarks and leptons. Vector bosons and graviton.
- Composite hadrons: Zoo of mesons and baryons begotten by QCD.
- Bethe-Salpeter Equation: A relativistic equation for bound-state problems.
- Path-integral formulation.
- Renormalization. The renormalizability of a theory is a key requirement.
- S-matrix: The unitary transformation chaacterizing a scaterring process.
- Constructive quantum field theory. Making quantum theory relativistic.
- Wightman axioms. Traditional basis for constructive quantum field theory.
- Mass gap. Infimum of the energies of states orthogonal to the vacuum.
- Coleman-Mandula theorem (1967).
- Haag-Lopuszanski-Sohnius theorem (1975).
- The Higgs mechanism gives elementary particles an intrinsinc mass.
- Yukawa interactions mediated by massive spinless particles.
- Klein-Gordon equation (1926). A second-order relativistic wave equation.
- Dirac wave equation (1928). This first-order equation predicts antimatter.
- Discovery of the positron by Carl Anderson (1930). The first antiparticle.
- Crossing symmetry: Antimatter is like matter going backward in time.
- Excess of matter over antimatter in the early Universe.
- Measuring chemical stuff in moles (mol) makes stoichiometry obvious.
- Modern distillation (alembic = still-head) is due to Mary the Jewess.
- The retort was a prominent tool of alchemists and chemists for centuries.
- Production and distillation of alcohol. Its origins and limitations.
- Black powder: An ancient explosive, still used as a propellant (gunpowder).
- Predicting explosive reactions: A useful but oversimplified rule of thumb.
- Thermite generates temperatures hot enough to weld iron.
- Enthalpy of Formation: The tabulated data which gives energy balances.
- Exothermic crystallization of sodium acetate trihydrate ("hot ice").
- Gibbs Function (free energy): Its sign tells the direction of spontaneity.
- Berthollet's Law of Mass Action governs every chemical equilibrium.
- Labile is not quite the same as unstable.
- Inks: India ink, atramentum, cinnabar (Chinese red HgS), iron gall ink, etc.
- Traditional pigments: Carbon black, vermillion, brazilin, malachite, etc.
- Beeswax is dominated by a long-chain ester (a "wax") called mycerin.
- Pine pitch & cedar pitch: Two similar products with different properties.
- Gum Arabic: The magic bullet of ancient chemistry.
- Ancient acids: From vinegar and lemon juice to vitriolic acid and more.
- Gold Chemistry: Aqua regia ("Royal Water") dissolves gold and platinum.
- Who was the "father" of modern chemistry?
- History of acidity: Mineral acids and organic acids.
- Muriatic acid or hydrochloric acid (HCl) is a strong acid.
- Sulfuric acid: Strong diprotic acid with weak second dissociation.
- Nitric acid ( aqua fortis ).
- Carboxylic acids: The weak organic acids (formic, acetic, etc.).
- Picric acid.
- Sulfonic acids are stronger than their carboxylic counterparts.
- Sulfamic acid.
- Bronsted acids: are donors of protons (1923).
- Lewis acids are acceptors of electron-pairs (1923).
- Hammett acidity function.
- Superacids: Stronger than pure sulfuric acid.
- Superbases have greater affinities for protons than the hydroxide ion.
- What is the strongest acid?
- Pure liquid water includes hydronium and hydroxide ions.
- In dilute solutions, the activity of water molecules is nearly constant.
- Arrhenius acids protonate water (Arrhenius, 1884).
- pH = -log( [H3O+] ) was introduced by Søren P.L. Sørensen in 1909.
- Diprotic acids have the same pH effect via either protonation.
- Polyprotic acids and bases and their associated dissociation polynomials.
- Titration curve: Sharp pH change at an acid-base neutralization point.
- Buffer solutions.
- Sulfurous acid: Sulfur dioxide solution, containing bisulfite and sulfite ions.
- Birth of organic chemistry: Urea was first made chemically in 1828.
- Aliphatic saturated hydrocarbons are called alkanes.
- Unsaturated hydrocarbons feature some carbons tied by multiple bonds.
- Acetylene and alkynes feature carbon atoms linked by a triple bond.
- Aomatic compounds feature 6 coplanar carbons in a ring.
- Carbohydrates (glucids) can be decomposed into carbon and water.
- Functional groups determine the basic reactions of organic chemistry.
- Oxocarbons (oxides of carbon). Organic chemistry without hydrogen.
- The oxidation number increases by oxidation and decreases by reduction.
- Salt bridges put solutions in electrical contact but prevent transfers of ions.
- Nernst equation: The voltage induced by different concentrations.
- Redox Reactions: Oxidizers are reduced by accepting electrons...
- Chemistry set from a bygone era (if memory serves).
- Basic glassware: Flasks, funnels, tubes, bulbs, condensers, etc.
- PTFE = Polytetrafluoroethylene = Teflon®.
- Ground-glass joints: Glass-to-glass conical joints have a 1:10 taper.
- Titration. Measuring the concentration of a reactant.
- Acidity color indicators. From litmus (1300) to
universal indicators (1933).
- Methylene blue as a redox indicator. The blue bottle experiment.
- Sugar dehydration with sulfuric acid. Black snake experiment.
- Waterlock: 1 g of sodium polyacetate can hold 825 mL of water.
- Negative-X: Water ignites a mixture of zinc and ammonium nitrate.
- Nitrogen triiodide Is an extremely unstable explosive when dry.
- The normal body temperature is 37°C (98.6°C) or is it?
- Normal blood pressure. Systolic (max.) and diastolic (min.) pressures.
- Normal pulse. 1 Hz (one hertz) is 60 beats per minute.
- Blood circulation (1628). Discovered by William Harvey (1578-1657).
- Respiration is a form of combustion (Lavoisier and Laplace, 1780).
- Normal caloric intake. 100 W of power is about 2065 kcal/day.
- International Unit (IU). Arbitrarily-defined rating of biological activity.
- Concentration is an amount (either mass or moles) per volume.
- Glycosylated hemoglobin (HbA1c) relates to average blood glucose (bG).
- Human fat. Gaining and losing weight. Metabolism.
- Body Mass Index (BMI, in kg/m2). Weight divided by square of height.
- Medical abbreviations commonly used in prescriptions and elsewhere.
- Mosquito-borne diseases: Malaria, dengue, chikungunya, etc.
- Propagation of epidemics. Analytic solution of the basic SIR model.
- Pandemic: To save the lives of others, get infected as late as possible...
- Caffeine is the most widely consumed psychotropic substance.
- Deflection of starlight by the Sun. What does General Relativity change?
- The Harress-Sagnac effect. Observer rotating with an optical loop.
- Relativistic rigid motion. Equilibrium modified at the speed of sound.
- In the Euclidean plane: Contravariance and covariance.
- In the Lorentzian plane: Contravariance and covariance revisited.
- Tensors of rank n+1 are linear maps that send a vector to a tensor of rank n.
- Signature of the quadratic form defined by a given metric tensor.
- Covariant and contravariant coordinates of rank-n tensors, in 4 dimensions.
- The metric tensor and its inverse. Lowering and raising indices.
- Partial derivatives along contravariant or covariant coordinates.
- Christoffel symbols: Coordinates of the partial derivatives of basis vectors.
- Covariant derivatives. Absolute differentiation. The nabla operator
Ñ.
- Contravariant derivatives: The lesser-known flavor of absolute derivatives.
- The antisymmetric part of Christoffels symbols form a fundamental tensor.
- Totally antisymmetric spacetime torsion is described by a vector field.
- Levi-Civita symbols: Antisymmetric with respect to any pair of indices.
- Einstein's equivalence principle implies vanishing spacetime torsion.
- Ricci's theorem: The covariant derivative of the metric tensor vanishes.
- Curvature: The Ricci tensor is a contraction of the Riemann tensor.
- The Bianchi identity shows that the Einstein tensor is divergence-free.
- The Weyl tensor is the traceless component of the Riemann tensor.
- Stress tensor: Flow of energy density is density of [conserved] momentum.
- Einstein's Field Equations: 16 equations in covariant form (Einstein, 1915).
- Free-falling bodies: Their trajectories are geodesics in curved spacetime.
- Gravitational lensing. How gravitation bends light.
- The "anomalous" precession of Mercury's perihelion is entirely relativistic.
- Schwarzschild metric: The earliest exact solution to Einstein's equations.
- van Stockum dust: A metric with closed timelike curves (Lanczos, 1924).
- What is mass?
- Unruh temperature experienced by an accelerating observer.
- Electromagnetism: Covariant expressions, using tensors.
- Kaluza-Klein theory of electromagnetism involves a fifth dimension.
- Harvard Tower Experiment: The slow clock at the bottom of the tower.
- Shapiro time delay: Effect on radar signals of gravitational time dilation.
- Warp drive. Traveling faster than light (FTL) ?
- Frame dragging. The effect predicted by Lense and Thirring in 1918.
- The Poynting-Robertson drag: Dust spirals inward around a bright star.
- Changes in the quadrupole moment of mass cause gravitational waves.
- The energy carried by G-waves first betrayed their actual existence (1974).
- PDH technique. Optical stabilization of the frequency of laser light (1983).
- LIGO: Laser Interferometer Gravitational-wave Observatory (since 1992).
- 2017 Nobel Prize for the detection of gravitational waves by LIGO.
- Olbers' paradox: The night sky isn't brightly lit. Why?
- Mach's principle: Local physics is determined by the whole Universe.
- Kant's Island Universes: The Universe is filled with separate galaxies.
- The Cosmological Principle: The Universe is homogeneous and isotropic.
- Medium-scale structure of the Universe: The foamy distribution of galaxies.
- The Big Bang: An idea of Georges Lemaître mocked by Fred Hoyle.
- The Cosmic Microwave Background (CMB): Its spectrum and density.
- Primordial nuclear soup: Hydrogen, Helium, Deuterium and Lithium.
- Cosmic redshift (z) of light from a Universe (1+z) times smaller than now.
- Multiple choices and misguided explanations for cosmic redshifts.
- Hubble Law relates redshift and distance for comoving points.
- Omega (W): The ratio of the density of the Universe to the critical density.
- Friedmann universe (1922). Its observed accelerating expansion (1998).
- Look-Back Time: The time elapsed since observed light was emitted.
- Distance: In a cosmological context, there are several flavors of distances.
- Comoving points follow the expansion of the Universe.
- The Anthropic Principle: An unsatisfactory type of absolute constraint.
- Dark matter & dark energy: Gravity betrays the existence of dark stuff.
- The Pioneer Anomaly: The anomalous braking of the Pioneer spaceprobes.
Galaxies and large-scale structure of the Universe
- The Milky Way is the name given to the star system that harbors our Sun.
- The local group is dominated by the Milky Way & Andromeda galaxies.
- The virgo cluster dominates our corner of the Universe.
- Superclusters are the largest objects in the Universe.
- Spiral galaxies. Andromeda and the Milky Way are examples..
- Ring galaxies a rare type of galaxies, difficult to classify.
- Elliptical galaxies Old galaxies. The largest we know is IC 1101.
- Supermassive black holes at the core of almost all galaxies...
- Nuclear fusion is what powers the stars.
- Brown dwarves glow from gravitational contraction. Fusion isn't ignited.
- Red dwarves can burn hydrogen for trillions of years.
- The Jeans mass. Above it, gases at temperature T collapse by gravitation.
- Main sequence: The evolution of a typical star.
- Metallicity (Z) measures the abundance of all elements beyond helium.
- The earlest stars (Population III) came from what the Big Bang produced.
- Eta Carinae and hypergiants. The most massive stars possible.
- Betelgeuse and red supergiants.
- Mira (Omicron Ceti). A very peculiar variable star.
- Rigel and blue supergiants.
- Planetary nebulae: Aftermaths of stellar explosions.
- White dwarfs: The ultimate fate of our Sun and other small stars.
- Neutron stars: Remnants from the supernova collapse of medium stars.
- Remnants of novae and supernovae associated with dated events.
- Stellar black holes form when supermassive stars run out of nuclear fuel.
- Primordial black holes. Substellar black holes left over from the Big Bang.
- Binary stars: Pairs of unlike stars often gravitate around each other.
- Binary X-ray source: A small accretor in tight orbit around a donor star.
- Astronomical unit (au). Successive definitions of a standard unit of length.
- Mean distance between the Sun and the Earth.nbsp; A tad above 1 au.
- Parsec: Triangulating interstellar distances, using the motion of the Earth.
- The solar corona is a very hot region of rarefied gas.
- The Carrington solar storm started on the 28th of August 1859.
- Solar radiation: The Sun has radiated away about 0.03% of its mass.
- The Titius-Bode Law: A numerical pattern in solar orbits?
- The 4 inner rocky planets: Mercury, Venus, Earth, Mars.
- Earth and Moon: This is home.
- The asteroid belt: Planetoids and bolids between Mars and Jupiter.
- The 4 outer giant gaseous planets: Jupiter, Saturn, Uranus, Neptune.
- Chiron and other centaurs have decaying orbits between the giant planets.
- Discovery of Neptune: Urbain Le Verrier scooped John Couch Adams.
- Pluto and other Kuiper Belt Objects (KBO).
- Sedna and other planetoids beyond the Kuiper Belt.
- What's a planet? The latest definition excludes Pluto.
- Heliosphere and Heliopause: The region affected by solar wind.
- Oort's Cloud is a cometary reservoir at the fringe of the Solar System.
- 'Oummuamua and Borisov. Interstellar objects visiting the Solar system.
- Long-term stability of the Solar system.
- The Butterfly Effect in Meteorology. (Edward N. Lorenz, 1962).
- The Feigenbaum constants: Bifurcation structure in the onset of chaos.
- Easy conversion between Fahrenheit and Celsius scales: F+40 = 1.8 (C+40)
Automotive :
- Fuel efficiency: (miles per gallon) × (liters per 100 km) = 235.21458333...
- Car speed is proportional to tire size & engine rpm, divided by gear ratio.
- 0 to 60 mph in 4.59 s, may not always mean 201.96 feet.
- Car acceleration. Guessing the curve from standard data.
- "0 to 60 mph" time, obtained from vehicle mass and actual average power.
- Thrust is the ratio of power to speed [measured along direction of thrust].
- Power as a function of chamber size for internal combustion engines.
- Optimal gear ratio to maximize top speed on a flat road (no wind).
Surface Areas :
- Heron's formula (for the area of a triangle) is related to the Law of Cosines.
- Archimedes' formula predates Heron by three centuries.
- L'Huilier's formula: Generalizing Heron's formula to spherical triangles.
- Brahmagupta's formula gives the area of a quadrilateral (cyclic or not).
- Bretschneider's formula for a quadrilateral of given sides and diagonals.
- Vectorial area of a quadrilateral: Half the cross-product of its diagonals.
- Parabolic segment: 2/3 the area of circumscribed parallelogram or triangle.
Volumes :
- Content of an horizontal cylindrical tank. given the height of the liquid in it.
- Volume of a spherical cap, or content of an elliptical vessel, at given level.
- Content of a cistern (cylindrical with elliptical ends), at given fluid level.
- Volume of a cylinder or prism, possibly with tilted [nonparallel] bases.
- Volume of a conical frustum: Formerly a staple of elementary education...
- Volume of any frustum when horizontal area is a cubic function of height.
- Volume of a sphere... obtained by subtracting a cone from a cylinder !
- Cavalieri's quadrature formula for the area under a power curve.
- The volume of a tetrahedron is the determinant of three edges, divided by 6.
- Volume of a wedge of a cone.
Averages :
- Filling a cistern with several canals. Problem 26 in the Jiuzhang Suanshu.
- Splitting a job evenly between two unlike workers.
- Splitting a job unevenly between two unlike workers.
- Mixing solutions to obtain a predetermined intermediate rating.
- Alcohol solutions are rated by volume not by mass.
- Mixing alcohol solutions to obtain an exact rating by volume (ABV).
- Vinegar is compared to a volumetric mix of pure acetic acid and water.
- Preparing solutions with hydrate salts. Example of citric acid.
- Special averages: harmonic (for speeds), geometric (for rates), etc.
- Mean Gregorian month: either 30.436875 days, or 30.4587294742534...
- The arithmetic-geometric mean is related to a complete elliptic integral.
Geodesy and Astronomy :
- Distance to the horizon is proportional to the square root of your altitude.
- Superior mirages. How objects beyond the horizon are brought into view.
- Distance between two points on a great circle at the surface of the Earth.
- Euclidean distance between two cities, along a line through the Earth.
- Geodetic coordinates: Point of elevation h at latititude
j and longitude q.
- The figure of the Earth. Geodetic and geocentric latitudes.
- Area of a spherical polygon. How to apply Girard's formula.
- Kepler's Third Law: The relation between orbital period and orbit size.
- Creation and Discovery in Science.
- Search for Extraterrestrial Intelligence. If we listen, we must talk.
- The Anthropic Principle: The laws of physics must allow human life.
- Science and Politics: Political support for Science makes a society worthy.
- What's Mathematics anyway? The groundwork of scientific knowledge.
- Life: The mysteries of evolution.
- Hominid speciess. The human family tree.
- Fossil calendars: 420 million years ago, a month was only 9 short days.
- LUCA: Last Universal Common Ancestor. A deep-sea creature.
- Geologic Time Scale (GTS): Beyond all human calendars.
Below are topics not yet integrated with the rest of this site's navigation.
- The Magnetic Field of the Earth.
- Life: The origins of life on Earth.
- Extraterrestrial life Is there intelligence out there?
- Nemesis: A distant companion of the Sun could cause periodical extinctions.
- Current Challenges to established dogma.
- Unexplained artifacts and sightings.
- The Riemann Hypothesis: {Re(s) > 0 &
z(s) = 0} Þ {Re(s) = ½}.
- Twin prime conjecture: One of the oldest open mathematical questions.
- Goldbach conjecture (1742): Any even number >2 is a sum of two primes.
- Legendre's conjecture There are primes between squares.
- Landau's fourth problem; Infinitely many primes follow a square.
- Schnizel's hypothesis H. Polynomials simultaneously prime infinitely often.
- P = NP ? Can we find in polynomial time what we can check that fast?
- Collatz sequences go from n to n/2 or (3n+1)/2.
Do they all lead to 1?
- The Poincaré Conjecture (1904). Proven by Grisha Perelman in 2002.
- Fermat's Last Theorem (1637). Proven by Andrew Wiles in 1995.
- The ABC conjecture (1985) of Joseph Oesterlé and David Masser.
- The union-closed sets conjecture (1979) of Péter Frankl.
- The Hadwiger conjecture in graph theory (1943).
- The Egyptian conjecture (1948) of Straus and Erdös.
- Birch and Swinnerton-Dyer conjecture about the rank of an elliptic curve.
- Gilbreath's conjecture was first formulated by François Proth in 1878.
- g-conjecture of McMullen (1970). Proved by Karim Adiprasito in 2018.
- Positive C2-diffeomorphisms on the circle. Do they form a simple group?
- Hadwiger-Nelson colorings are such that 2 like points are never 1 unit apart.
- The only magic hexagon.
- The law of small numbers applied to conversion factors.
- Quadratic formulas yielding long sequences of prime numbers.
- The area under a Gaussian curve involves the square root of p
- Exceptional simple Lie groups.
- Monstrous Moonshine in Number Theory.
- Oldest open
mathematical problem: Are there any odd perfect numbers?
- Magnetic field of the Earth:
South side is near the geographic north pole.
- From the north side,
a counterclockwise angle is positive by definition.
- What initiates the wind?
Well, primitive answers were not so wrong...
- Why "m"
for the slope of a linear function y = m x + b ? [in US textbooks]
- The diamond mark on US tape measures
corresponds to 8/5 of a foot.
- Naming the largest possible number,
in n keystrokes or less (Excel syntax).
- The "odds in favor" of poker hands:
A popular way to express probabilities.
- Reverse number sequence(s)
on the verso of a book's title page.
- Living species:
About 1400 000 have been named, but there are many more.
- Dimes and pennies:
The masses of all current US coins.
- Pound of pennies:
The dollar equivalent of a pound of pennies is increasing!
- Nickels per gallon:
Packing more than 5252 coins per gallon of space.
- Geodetic coordinates,
based on the Reference Ellipsoid defined in 1980.
- Geocentric coordinates
are almost never used in geography or astronomy.
- Distance from the center of the Earth
to points located at the surface.
- The volume of the Grand Canyon:
2 cm (3/4") over the entire Earth.
- The Oldest City in the World:
Damascus or Jericho?
- USA (States & Territories):
Postal and area codes, capitals, statehoods, etc.
- Inventing Money: Brass in China, electrum in Lydia, gold and silver staters.
- Prices of Precious Metals: Current market values (Gold, Silver. Pt, Pd, Rh).
- Medieval system: 12 deniers to a sol.
- Ancien Régime French monetary system.
- British coinage before decimalization.
- Exchange rates when the euro was born.
- Worldwide circulation of currencies.
Bitcoin (BTC) and other crypto-currencies
- What are bitcoins?
- Who invented bitcoins? Who is Satoshi Nakamoto ?
- Blockchain, hashpuzzles, Merkle trees, public/private-key cryptography.
- Counterfeit Coin:
In 3 weighings, find an odd object among 12, 13 or 14.
- Counterfeit Penny Problem:
Find an odd object in the fewest weighings.
- Explicit tables for detecting
one odd marble among 41, in 4 weighings.
- Find-a-birthday:
Detect an odd marble among 365, in 6 weighings.
- Error-correcting codes for ternary numeration.
- If the counterfeit is known to be heavier,
fewer weighings may be sufficient.
- Calendrical ratios and their slow evolution with time.
- Julian Day Number (JDN). Counting days in the simplest of all calendars.
- The Week has not always been a period of seven days.
- Egyptian year of 365 days: Back to the same season after over 1500 years.
- Heliacal rising of Sirius: Sothic dating.
- Coptic Calendar: Reformed Egyptian calendar based on the Julian year.
- The Julian Calendar: Year starts March 25. Every fourth year is a leap year.
- Anno Domini: Counting roughly from the birth of Jesus Christ.
- Gregorian Calendar: Multiples of 100 not divisible by 400 aren't leap years.
- Counting the days between dates, with a simple formula for month numbers.
- Age of the Moon, based on a mean synodic month of 29.530588853 days.
- American names of full moons are inherited from Algonquian tribes.
- Blue Moon is a term which has been defined in two different ways.
- Easter Sunday is defined as the first Sunday after the Paschal full moon.
- The Muslim Calendar: The Islamic (Hijri) Calendar (AH = Anno Hegirae).
- The Jewish Calendar: An accurate lunisolar calendar, set down by Hillel II.
- Zoroastrian Calendar.
- The Zodiac: Zodiacal signs and constellations. Precession of equinoxes.
- The Iranian Calendar. Solar Hejri [SH] or Anno Persarum [AP].
- Enkutatash (Sept. 11 or 12) of Julian year N begins Ethiopian year N-7.
- The Chinese Calendar.
- The Japanese Calendar.
- Mayan System(s): Haab (365), Tzolkin (260), Round (18980), Long Count.
- Indian Calendar: The Sun goes through a zodiacal sign in a solar month.
- Post-Gregorian Calendars: Painless improvements to the secular calendar.
Roman Numerals
(Archaic, Classic and Medieval)
- Roman Numeration:
Ancient rules and medieval ones.
- An easy conversion table
for numbers up to 9999.
- Larger Numbers, like 18034...
- Extending the Roman system.
- The longest year so far, in terms of Roman numerals.
- IIS (or HS) is for sesterce
(originally, 2½ asses, "unus et unus et semis").
- Roman fractions.
A rudimentary duodecimal system.
- Standard jokes.

- Limericks.
- Proper credit may not always be possible.
- Trick questions can be legitimate ones.
- Ignorance is bliss: Why not read all that mathematical stuff faster ?
- Silly answers to funny questions.
- Why did the chicken cross the road? Scientific and other explanations.
- Humorous or inspirational quotations by famous scientists and others.
- One great quote to be translated into as many languages as possible.
- Famous Last Words: Proofs that the guesses of experts are just guesses.
- Famous anecdotes.
- Parodies, hoaxes, and practical jokes.
- Omnia vulnerant, ultima necat: The day of reckoning.
- Funny Units: A millihelen is the amount of beauty that launches one ship.
- Funny Prefixes: A lottagram is many grams; an electron is 0.91 lottogram.
- The Lamppost Theory: Only look where there's enough light.
- Is it insanity or just a viable alternative to orthodoxy?
- Anagrams: Rearranging letters may reveal hidden meanings.

- Mnemonics: Remembering things and/or making fun of them.
- Acronyms: Funny ones and/or alternate interpretations of serious ones.
- Usenet Acronyms: If you can't beat them, join them (and HF, LOL).
- Adobe's Symbol font: Endangered standard HTML mathematical symbols.
- The equality symbol ( = ). The "equal sign" dates back to the 16th century.
- The double-harpoon symbol denotes chemical equilibrium.
- Line components: Vinculum, bar, solidus, virgule, slash, macron, etc.
- The infinity symbol ( ¥ ) introduced in 1655 by John Wallis (1616-1703).
- Transfinite numbers and the many faces of mathematical infinity.
- Chrevron symbols: Intersection (highest below) or union (lowest above).
- Disjoint union. Square "U" or inverted p symbol.
- Blackboard bold: Doublestruck characters denote sets of numbers.
- The integration sign ( ò ) introduced by Leibniz at the dawn of Calculus.
- Evaluation bar. Difference betwen the values of an expression at two points.
- The end-of-proof box (or tombstone) is called a halmos symbol (QED).
- Two "del" symbols: ¶ for partial derivatives, and
Ñ for Hamilton's nabla.
- A strange lowercase p (Ã) used only for
Weierstrass elliptic functions.
- The rod of Asclepius: Medicine and the 13th zodiacal constellation.
- The Caduceus: Scepter of Hermes, symbol of commerce (not medicine).
- Tetractys: Mystical Pythagorean symbol, "source of everflowing Nature".
- The Borromean Rings: Three interwoven rings which are pairwise separate.
- The Tai-Chi Mandala: The taiji (Yin-Yang) symbol was Bohr's coat-of-arms.
- Dangerous-bend symbol: Introduced by Bourbaki, popularized by Knuth.

Monographs and Complements
- About Zero.
- Wilson's Theorem.
- Counting Polyhedra:
A tally of polyhedra with n faces and k edges.
- Sagan's number: The number of stars,
compared to earthly grains of sand.
- The Sand Reckoner: Archimedes fills the cosmos
with grains of sand.

- Numericana's list
of distinguished Web authors in Science...
- Giants of Science:
Towering characters in Science history.
- Two Solvay conferences
helped define modern physics, in 1911 and 1927.
- Physical Units:
A tribute to the late physicist Richard P. Feynman.
- The many faces of Nicolas Bourbaki
(b. January 14, 1935).
- Lucien Refleu
(1920-2005). "Papa" of 600 mathematicians. [ In French ]
- Taupe Laplace. [ In French ].
- Roger Apéry (1916-1994)
and the irrationality of z(3).
- Hergé (1907-1983):
Tintin and the Science of Jules Verne (1828-1905).
- Other biographies: Dulong, Galois, Tannery, Vessiot,
Drach, Glénisson...
- Escutcheons of Science (Armorial):
Coats-of-arms of illustrious scientists.

In-Depth Reviews of Great Products
- BASIC Stamp® HomeWork Board™ USB: Review and first baby steps.
- Decoding a digital PWM signal with a low-pass filter.
- Volume control obtained by attenuating a PWM signal before filtering.
- Using an LCD display (HD44780) without built-in PBASIC commands.
- A keypad for independence: Cutting off the umbilical USB cord.
- Cheapest sonar sensor uses two I/O pins (where one would suffice).
- The I2C bus. Example: Interface with a real-time clock (RTC).
- Genuine Arduino starter kit: All you need for a hands-on guided tour.
- The Arduino Uno: The unit which started it all (now in Revision 3 ).
- Arduino Leonardo & Micro don't use separate processors for USB.
- Chameleon: An Arduino clone and a Parallax Propeller on one board.
- Pro and cons of Arduino clones: Avoid them as a first purchase.
- Buyer beware: G8A92AA has wireless connectivity, NW80AA doesn't.
- Setup: Language, unique name, numerical and calendrical formats.
- Connectivity. How HP Prime calculators communicate with PCs.
- HP StreamSmart. Four-port data streamer capable of 5700 samples / s.
- Hacking the HP Prime. Possible DIY hardware modifications.
- Two calculators in one. A numerical workspace next to a separate CAS.
- Reverse Polish Notation (RPN) is only an option in the "Home" mode.
- The RPN stack is more than a read-only record of previous entries & results.
- Objet-oriented functions behave according to the nature of their arguments.
- CAS. The Computer Algebra System of Bernard Parisse.
- Apps. Blue icons denote graphical applications with similar structures.
- User functions. A single-expression definition may involve conditionals.
- Programming, using the HP Prime Programming Language (HP PPL).
- User-defined apps.
- Unit conversions. The HP Prime features 167 basic units and 20 prefixes.
- Constants of Nature. 23 built-in physical constants and many others.
- Lists and list-processing primitives. Not all list manipulations are possible.
- Vectors and matrices. Multidimensional linear algebra.
- Polynomials. Algebra on polynomials & special predefined polynomials.
- Calendrical functions. Dates are encoded as decimal numbers: yyyy.mmdd
- Special Functions. Beyond trigonometric and hyperbolic functions.
- Galois Fields. An almost undocumented buggy feature of the HP Prime.
- Easter Eggs. "Visit Plot Gallery".
- Kudos and Gripes. Likes and Dislikes. Deal-breakers. Bug reports.
- Fixed bugs and new kudos.
- Printer : The HP 82240B thermal printer has been standard since 1989.
- Modifier keys. Lesser-used functions require several keystrokes.
- Infinity: Unsigned algebraic infinity and signed topological infinities.
- Physical units: A built-in feature inherited from the HP-28 (1986).
- Bug reports: Severe problems and minor ones.
- Complex functions: Complex values & arguments. Complex variables.
- RPL programming ("Reverse Polish LISP") originated with the HP-28.
- Easter eggs: Unofficial features, play Tetris® or MineHunt.
HP-35s: Released on the 35th birthday of the HP-35
- Modifier keys.
Lesser-used functions require several keystrokes.
- Reverse Polish Nptation (RPN) was invented by Jan Lukasiewicz in 1924.
- Unit conversions: °F/°C | HMS |
°/rad | lb/kg | mi/km | in/cm | gal/L.
- 40 physical constants (and one mathematical constant) in a single menu.
- Bug reports: Severe problems and minor ones.
- Complex functions:
Complex values & arguments. Complex variables.
- Programming:
Recorded keystroke sequences. Tests, loops & subroutines.
- Modifier keys. Lesser-used functions require several keystrokes.
- Physical units: A very nice afterthought, with a few rough edges.
- Analytical functions may present discontinuity cliffs in the complex realm.
- Wrong! 0 to the 0th power should be 1. ¥
and +¥ shouldn't be equal.
- 68000 Assembly Programming: A primer without the help of an assembler.
- The clock frequency of your calculator measured with 0.1% accuracy.
- TI's BASIC. A built-in interpreted language not designed for speed.
- Pretty 2D algebraic displays can only be edited in their 1D version.
- The keypad:
One shift-key suffices with the introduction of multi-tap.
- Integer arithmetic.
Numbers with more than 6 digits cannot be factorized.
- 20 pairs of unit conversions...
and not a single inaccuracy. (That's rare!)
- 20 physical constants
listed by name, with their units. 9 are numbered.
- Bug reports: From minor gripes to more severe flaws.
- Side-by-side comparison of the fx-991EX and fx-991ES PLUS models.
- fx-991ex. The EX series is an improvement on the best-selling ES series.
- History of the "natural" Casio scientific calculator ES series.
- Mode 4: Hexadecimal or octal arithmetic on 32-bit integers.
- Mode 7: Tabulate a function (or a pair of functions with "plus" version).
- Scientific constants: Consistent values recommended by CODATA (2010).
- Conversion factors between units: A few inaccuracies & one typo.
- The line of Sharp scientific calculators.
What the model numbers mean.
- The basics. Color-coded multiple functions.
- Entering and exiting special modes.
- Solving cubic equations.
- The basics.
- The good and the bad.
- Nikon glossary. Terms, symbols and abbreviations used by Nikon.
- Evolution of Nikon DX Digital Cameras, from the D50 to the D500.
- Buyer's Guide to all Nikon DX cameras: D3x00, D5x00, D7x00 and D500.
- Frames per second: The D5500 can shoot at a top rate of exactly 5 fps.
- DX sensors:
23.46 x 15.64 mm (3.91m/p) or 23.49 x 15.66 mm (4.2 m/p).
- Back-button focusing. A good customization to make on any camera.
- White balance: Compensating for the color of incident light.
- Setting up a focus trap.
- Commander mode with SB-500 Speedlight, using third-party flash units.
- Remote control: Infrared (ML-L3) or cable-release (with timer).
- GPS modules communicate using the NMEA 0183 standard protocol.
- External power. Connector (AP-5a) & AC adapter (AH-5) are separate.
- Tripods & monopods: Basic tripod, versatile travel tripod, hiking stick.
- Camera straps.
- Camera bags and cases.
- A short history of Nikon lenses.
- Automatic extension tubes allow an ordinary lens to be used close-up.
- Attach a lens backwards to the camera body, or in front of another lens.
- Low-light normal lens: Nikon 35mm f/1.8G AF-S DX (54 mm reach).
- Fast portrait lens Nikon 50mm f/1.8G AF-S (77 mm DX reach).
- Long macro (130 mm DX reach): Nikon 85mm f/3.5G AF-S DX ED VR.
- Overview of other portrait lenses. Long lenses with wide apertures.
- Superzoom: Nikon 18-300mm f/3.5-6.3G AF-S DX VR (28-460 reach).
- Kit lens and compact telephoto zoom tandem: Nikon 18-55 and 55-300mm.
- Telephoto zoom AF-S Nikkor 200-500mm f/5.6E ED VR (307-767mm).
- Fast (f/2.8) Tokina wide zooms: 11-16mm (17-25) and 11-20mm (17-31).
- Ultrawide Samyang fisheye lens: Rokinon 8mm f/3.5 AE (for Nikon).
- Bayonet hoods don't interfere with native filters (without step-up rings).
- Telescope converter: Turning any F-mount lens into a spotting scope.
- Lens pinout: Electrical connections between Nikon bodies and lenses.
- Lens identifiers: Database of F-Mount Nikon-compatible digital lenses.
- EXIF: The hidden data attached to every JPEG the camera makes.
- Mamiya 645 1000S. A complete vintage system on eBay.
- Mamiya-Sekor C lenses: Interchangeable lenses for the M645.
- Battery: Silver-oxide is usually better than lithium.
Alkaline isn't so good.
- Meniscus lens. Wollaston landscape lens.
- No. 2 Brownie, Model F. The first all-metal Brownie (1924).
Photographic Film: The soul of the twentieth century.
- Ongoing legacy of analog photography: Film is dead, long live Film.
- What makes silver so special. The miraculous chemistry of silver.
- The latent image. It's true nature remained a mystery for decades.
- The magic of photographic emulsions. How silver captures light.
- C-41 film processing and proof printing at different professional labs.
- "Develop and Scan" services kill the advantage of medium-format film.
- Film scanner: A $170 flatbed capable of scanning 120-film at 9600 dpi.
- Black-and-white film: Ilford, Kodak, Agfa (Rollei) and one Fuji offer.
- Rollei infrared film: Processing film based on a flimsy polyester base.
- Processing black-and-white film at home. Lots of room for creativity.
- Paterson System 4. Tanks, self-loading reels and force film washer.
- Developer. The most critical bath in photographic processing.
- Stop-bath. An acidic stop-bath puts an abrupt end to the developer's action.
- The fixer stabilizes the image by dissolving unused light-sensitive material.
- Washing with (bisulfite) salts makes a fresh-water rinse more efficient.
- Spotless drying can be achieved with a wetting agent in the final rinse.
- History of natural-color reproduction: The path to modern color films.
- Color negative films: Kodacolor, Ektar, Agfacolor, Fujicolor.
- C-41 processing of color negatives is best left to professional machines.
- Color reversal films (slides). Kodachrome (K-14). Ektachrome (E-6).
- Movies & Video. Capturing motion with a sequence of images.
- Video formats, resolution, color depth and bit rates.
- Video Lighting: Color balance, power. LED panel, COB and HMI.
- Camera support gear: Monopods and tripods.
- 3-axes motorized gimbal mount.
- Panasonic Lumix hybrids cameras. The GH5 offers great video features.
- Firmware updates and unlocks. GH5 camera, lenses and XLR audio adapter.
- Neutral density (ND) filters are essential when shooting video.
- Olympus M.Zuiko Digital ED 7-14mm f/2.8 Best MFT wide-zoom lens.
- Panasonic 8-18mm f:2.8-4.0. Best MFT lens of 2017, for many reviewers.
- Panasonic 12-60mm f:2.8-4.0. Most popular kit lens for the GH5.
- Lumix G Leica DG Nocticron 42.5mm f:1.2. Best lens for still portraits.
- Panasonic 50-200mm f:2.8-4.0. Best telephoto zoom for the GH5.
- Panasonic 100-400mm f:4.0-6.3. Super-telephoto zoom. 800 mm reach.
- Proper cinema lenses (no focus breathing). Veydra mini-primes.
- Flash strobes. Some TTL flash units for shooting stills with the GH5.
- Customizing a GH5 camera cage with the SmallRig system.
- DIY no-stich hand strap (with accessory pouch) for camera cages.
- Micro four-thirds (MFT or M43). Open standard for mirrorless cameras.
- Adapters & converters allow MFT cameras to use reflex-mount lenses.
- Serial Digital Interface (SDI). Coaxial cables and locking connectors.
- High-Definition Multimedia Interface (HDMI). The consumer standard.
- Atomos recorders/monitors: Shogun Inferno, Ninja Inferno, Ninja V.
- Monitors and colorimeters to deliver accurate color reproduction.
- CODEC standards. COmpression and DECpmpression of video signals.
- Look-Up Table (LUT). The ultimate customization of color information.
- Editing & post-production. Modifying clips and putting them together.
- Montage.
- Tips from successful YouTubers.
- Teleprompters. The key to smooth on-camera speech delivery.
- Microphones: A brief summary of our dedicated page on the topic.
- Evolution of sound recording. From soot, tinfoil and wax to 24-bit audio.
- Rooms acoustics. Suppressing outside noise. Trapping unwanted reverb.
- Reverbs and delays. Natural and synthetic reverberation and echoes.
- Pop filters. Pop screens suppress plosives and shield against spit...
- Microphone stands & booms. The most common thread mount is 5/8''-27.
- Audio connectors: Phone jacks (¼'', 3.5mm, 2.5mm) and balanced XLR.
- Microphone cable: Balanced line formed by a shielded twisted pair.
- Volume: Sound level, normalized to current broadcast standards.
- Equalization (EQ). Adjusting the frequency response for fidelity or effect.
- AGC, limiters and compressors: Best use of a limited dynamic range.
- Preamplifiers. Converting a microphone output into a usable line signal.
- Analog low-pass filtering is paramount before digitization of any signal.
- Analog-to-digital conversion (ADC).
- Digital-to-analog conversion (DAC).
- Generation loss. Signal degradation due to each ADC/DAC pair.
- Digital wireless systems: Sennheiser, Røde, Sony, Saramonic, Azden.
- The DMW-XLR1 provides the GH5 camera with two 24-bit audio channels.
- Analog mixer. Mixing sound from several audio sources in real-time.
- Direct insertion (DI) boxes intercept a clean signal between guitar and amp.
- Audio impedance transformers. Step-up to use a mic with a guitar amp.
- Match an output impedance with a load equal to its complex conjugate.
- Handy audio recorders: Zoom H1, H1n, H2n, H4n Pro, H5, H6 (and F1).
- Zoom H1 ultra-portable recorder: Single-channel and built-in stereo mic.
- Zoom H5 four-channel recorder: XLR inputs & interchangeable capsules.
- Audio interfaces between various audio signals and a digital computer.
- The Art of Slating: Clapboard conventions and etiquette.
- Soundtrack. Affordable licensing of music for amateurs.
- Foley, sound effects and sound design.
- Voice-over. Crafting spoken words off-camera. Dog-clicker editing.
- Digital audio workstation (DAW). Putting it all together...
Microphones : Fundamental Issues and Buyer's Guide
- Sound What pressure waves entail. Thermodynamics of acoustics.
- Classifying microphones according to which physical quantity they exploit.
- Unified theory of inductive (dynamic) and condenser microphones.
- Noise-floor: What's left when the interesting stuff is gone.
- Microphone sensitivity (mV/Pa): voltage output to sound pressure input.
- Pickup patterns: Omnidirectional, figure-8, cardioid, and beyond...
- Dual-diaphragm microphones allow switchable or variable pickup patterns.
- Compound microphones with adjustable frequency response..
- Calibrated measurement microphones. Testing acoustics and audio gear.
- Attenuation pad switch allows a microphone to record louder sounds.
- High-pass filter (HPF). A switchable option built into many microphones.
- Characteristics of full-size wired microphones. Capacitive or inductive.
- Acoustic properties of large diaphragms. Resonances and pickup patterns.
- Large-diaphragm condenser microphones (LDC). Studio microphones.
- Dynamic microphones. Rugged stage microphones with limited bandwidth.
- Ribbon microphones. Special dynamic type, with output transformers.
- Small-diaphragm pencil microphones are often available in matched pairs.
- Shotgun microphones. Highly-directive narrow condenser microphones.
- Lavalier microphones (lapel mics) isolate the speaker from ambient sound.
|
Note:
The above numbering may change, don't use it for reference purposes.
|
Noted
Numericana fans
(and/or contributors) in alphabetical order:
- Max Alekseyev, Silent Circles.
- Stuart Errol Anderson, Enumeration of Polyhedra.
- Gottfried Barthel, Generic Carmichael Numbers.
- David Cantrell, Perimeter of an Ellipse
(2001, 2004, etc.)
- Scott Cram, Magician
(Grey Matters).
- Joe Crump, Carmichael Divisors.
- Paul Godfrey, Lanczos Formula.
- Michel Marcus, Hemiperfect Numbers
(11/2,
13/2,
15/2,
17/2).
- Ed Pegg, Jr. Recreational Mathematics
(MathPuzzle).
- Belisha Price, Polyhedra.
- Knud Thomsen, Surface Area of an Ellipsoid.
- Robin Whitty, Theorems.

- Jochen Wilke, Escutcheons of Science.
Guest Authors:
Public-Domain Texts:
|